初中几何三角形难题(初中几何三角形知识点大全)

导语：通过一道有趣的几何题，学习初中三角形问题解题的思路

初中几何中，三角形的相关问题是考试的重点之一。下面通过一道有趣的几何题学习解题的思路。

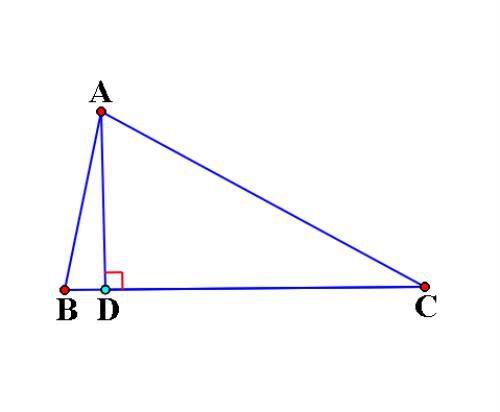
如图，△ABC中，∠B=75°，AD⊥BC。若BC=2AD，求∠C的度数。

分析：已知∠B=75°，则∠BAD=15°，虽然是特殊角，但还不够特殊，解题中需要的是30°、45°或者60°这样的角。

自然就想到两个思路：从∠B割出15°，或者给∠BAD再加上15°。

这里我们用后者来解题。

过点A作线段AE使得∠BAE=15°，交CB延长线于点E。如图所示。

则在Rt△ADE中，∠EAD=30°，∠E=60°。

再由已知条件BC=2AD，不妨设AD=√3，

则BC=2√3，易得ED=1，AE=2。

因为AB是∠EAD的平分线，

所以有AD/AE=BD/EB（角平分线定理），即：

√3/2=BD/1-BD

解得BD=2√3-3。

所以CD=BC-BD=2√3-(2√3-3)=3。

观察Rt△ADC中，AD=√3,DC=3，很明显∠C=30°。

小结：通过分析题目已知条件，构建特殊角是解三角形问题的核心。本解法中用到了角平分线定理。如果换从∠B中割去15°构建一个60度角也可解题。本题另一处是直接设AD=√3，相比用字母表示，可简化计算。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小美创作整理编辑！