已知三角形三边的长度求面积(已知三角形三边长怎么求面积)

导语：已知三角形三边的长，怎样求三角形的面积？我们来推导求面积公式

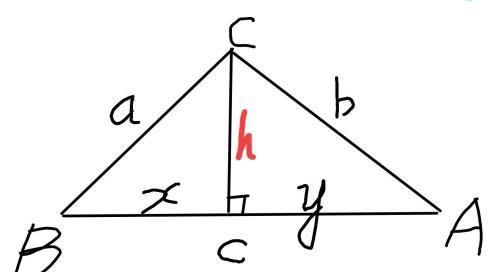
很多时候，我们知道三角形三边的长，要求三角形的面积。你知道怎样求吗？

设三角形三边长为a、b、c，作c边上的高h把c分成两段x和y。我们的做法是先求出高h的长度，进而用最基本的面积公式S△ABC=ch/2求出三角形的面积。

三角形面积公式推导

由勾股定理得：

a²-x²=b²-y²，①

x+y=c。②

②代入①得：

a²-x²=b²-(c-x)²=b²-c²-x²+2cx，

x=(a²+c²-b²)/2c。③

③代入②得：

y=(b²+c²-a²)/2c。④

我们用③或④都可以求出h。

h²=a²-x²

=a²-((a²+c²-b²)/2c)²

=(2a²b²+2b²c²+2c²a²-a⁴-b⁴-c⁴)/4c²

这样得到的h有四次方，数据比较大，不太好算。我们可以想办法化成好算的形式。

我们看它的分子部分：

2a²b²+2b²c²+2c²a²-a⁴-b⁴-c⁴

这是一种对称形式，应该可以分解因式。那么，怎样去分解因式呢？

我们先考察以下多项式的平方：

(a²+b²+c²)²

=a⁴+b⁴+c⁴+2a²b²+2a²c²+2b²c²，

(a²+b²-c²)²

=a⁴+b⁴+c⁴+2a²b²-2a²c²-2b²c²，即

-(a²+b²-c²)²

=-a⁴-b⁴-c⁴-2a²b²+2a²c²+2b²c²，

这个有点像，还有一个项符号不同。

等式两边同时加上4a²b²：

4a²b²-(a²+b²-c²)²

=-a⁴-b⁴-c⁴+2a²b²+2a²c²+2b²c²

所以有

-a⁴-b⁴-c⁴+2a²b²+2a²c²+2b²c²

=4a²b²-(a²+b²-c²)²

=(2ab+a²+b²-c²)(2ab-a²-b²+c²)

=((a+b)²-c²)(c²-(a²-b²))

=(a+b+c)(a+b-c)(c+a-b)(c-a+b)

所以，

h²=(a+b+c)(a+b-c)(c+a-b)(c-a+b)/4c²，

h=√((a+b+c)(a+b-c)(c+a-b)(c-a+b))/2c，

S△ABC=ch/2

=√((a+b+c)(a+b-c)(c+a-b)(c-a+b))/4。

这个三角形面积公式没有平方项，比较好算。

还可以把4放进根号里面继续化简：

S△ABC

=√(((a+b+c)(a+b-c)(c+a-b)(c-a+b))/16)

=√(((a+b+c)/2)((a+b-c)/2)((c+a-b)/2)((c-a+b)/2))

=√(((a+b+c)/2)((a+b+c-2c)/2)((c+a+b-2b)/2)((c+a+b-2a)/2))

(a+b+c)/2是周长的一半，记为p，则

S△ABC=√(p(p-a)(p-b)(p-c))。

这就是著名的海伦公式。这种形式计算量最小，也比较好记。

总结一下：在推导用三角形的三边长求三角形的面积时，在化简过程中遇到分解因式，最终化成比较简便的形式，便于计算和记忆。

本文内容由快快网络小春整理编辑！