中考几何题目经典的辅助线手法(初中几何辅助线口诀大全)

导语：中考几何进阶 辅助线法则（12）角度分析是不二的法门：归纳

中考几何进阶 辅助线法则（12）角度分析是不二的法门：归纳

几何分析方法，有正向分析：从已知条件出发向所求靠拢的逻辑推理；和逆向分析：从所求向已知条件靠拢的逻辑推理。通常都是二者综合起来运用的。

分析的技术手段，分为三大类：角度分析、线段分析、面积分析。

依据特点分类，有保形变换（全等变换）、保角变换（相似变换）、和保面积变换。

从形式上，就是辅助线，但实质目的，往往是构造“辅助角”。无论是平行线、角分线、还是线段垂线或者垂直平分线、或者其它的辅助线，无非是构造一些“特殊三角形”，包括等腰、等边、全等、相似、直角三角形等，牵涉到的都有角度的转移、分割、合并。

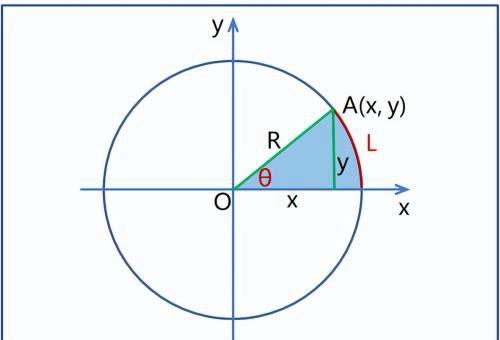
角度分析的重要性，还可以从角度的本质来看。如图，角度的定义是扇形所对的弧长与半径之比：

重要的是这个比值和半径大小无关；当半径保持不变时，θ和弧长成正比。这就是角度的本质：它是线段之比。所以在直角三角形中，θ一定时，各线段比值保持不变，和线段的长度无关。

角度分析相关性质

1) 相交线所成的角中，对顶角相等，邻角互补。/ 2) 与平行线相交的直线截得同位角相等、内错角相等、同旁内角互补。/ 3) 等腰三角形的底角相等；底边的中线分等腰三角形为两个全等直角三角形。/ 4)直角三角形的两个锐角互余。/ 5) 三角形内角和等于180°。/ 6) 外角定理：三角形一个外角等于两个不相邻内角和。/ 7) 平行四边形的对角相等，同旁内角互补。/ 8) 梯形的同旁内角互补。/ 9) 等腰梯形的底角相等。/ 10) 菱形的对角线分菱形为四个全等直角三角形，即对角线互相垂直平分。/ 11) 正多边形的内角全等。/ 12) 多边形的外角和等于360°。/ 13) 多边形的内角和＝(n－2)×180°。/ 14) 等量加等量还是等量。/ 15) 同弧上的圆周角相等。/ 16) 同弧上的圆心角相等。/ 17) 直径上的圆周角等于90°。/ 18) 相似或全等三角形对应角相等。/ 19) 对称与折叠的性质。

线段分析相关性质

1）两平行线间距离处处相等。/ 2）线段垂直平分线上的点到线段两端的距离相等。/ 3）角平分线上的点到角的两边的距离相等。/ 4）等腰三角形的两个要想等。/ 5）正多边形的边相等。/ 6）等腰梯形的两个腰相等。/ 7）平行四边形的对边相等。/ 8）平行四边形的对角线互相平分。/ 9）菱形的四个边相等。/ 10）菱形的对角线互相垂直平分。/ 11）全等三角形的对应边相等。/ 12）中点连线定理：三角形的中点连线平行且等于底边的一半。/ 13）平行线分线段成比例定理。/ 14）相似三角形对应边成比例（包括中线、角平分线、高、外接圆半径、内切圆半径等等）。/ 15）角平分线定理。/ 16）射影定理。/ 17）勾股定理。/ 18）解直角三角形。/ 19）圆幂定理。/ 20）对称与折叠的性质。

角度分析无处不在，后续几篇通过一些例子，体会角度分析的重要性。

---------

例题 （待续。。。。。。）

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！