中考几何题目经典的辅助线手法(初中数学几何常见辅助线作法口诀)

导语：中考几何进阶 03 辅助线法则（3）

中考几何进阶 03 辅助线法则（3）

四边形，对边等，中点连线是等腰；《法则 二》

（1）四边形ABCD，对边AB＝CD，则某一对角线中点与另一对对边中点的连线构成等腰三角形。

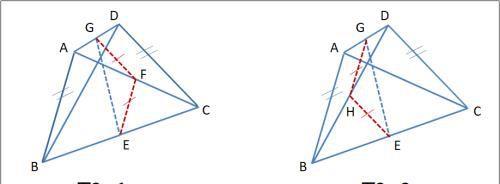
如图2—1，E\F\G为各线段中点，△FEG为等腰三角形（FE＝FG＝AB/2）。

或图2—2，E\G\H为各线段中点，△HEG为等腰三角形（HE＝HG＝AB/2）。

或图2—3，是将上述两图合并，EFGH是菱形，EG⊥FH且平分。

（2）一种退化的情景是点A、D、C共线（AB＝CD）：E\G\H为各线段中点，△HEG为等腰三角形（HE＝HG）。如图2—4所示。

中点线，线缩半，平行移动成折线；《法则 三》

中点连线的另一重要作用是将分离的线段缩半、平移成折线，从而构成三角形。如图2—1至图2—4所示。

----------

例题 如图，D是△ABC内一点，延长BA至点E，延长DC至点F，使得AE＝CF。G、H、M分别是BD、AC、EF的中点。如果G、H、M三点共线，求证：AB＝CD。

〖分析〗

求证相等的两线段相距甚远，但是题设有诸多中点。通过中点连线可将各相关线段 缩半 平移。

和AB相关的是△ACB，过线段AC中点H的中点连线HN，其中N是BC中点，则HN∥＝AB/2；

和CD相关的是△BDC，过线段BD中点G的中点连线GN。GN∥＝CD/2。

现在问题转换为求证△NGH为等腰三角形，即HN＝GN。

题设中有一对对边相等的四边形ACFE，那么对角线AF的中点P与另一对对边AC、EF中点的连线构成一个等腰三角形，即△PHM为等腰三角形：∠PHM＝∠PMH。其中PH∥＝CF/2；PM∥＝AE/2；而AE＝CF，∴PH＝PM。

由平行关系：GN∥CD（CF）∥PH，∴∠ HGN＝∠PHM（同位角）；HN∥AB（AE）∥PM，∴∠GHN＝∠PMH（同位角）

这样，因为∠PHM＝∠PMH，就有∠ HGN＝∠GHN，△NGH是等腰三角形，HN＝GN。于是AB＝CD。

本题也是一道竞赛题。如果不是10条辅助线法则，一时无从思考。但对10条法则熟练地化，本题再也不是什么难题了。

本文内容由小里整理编辑！