利用等高模型求面积的公式(利用等高模型求面积怎么求)

导语：利用等高模型求面积

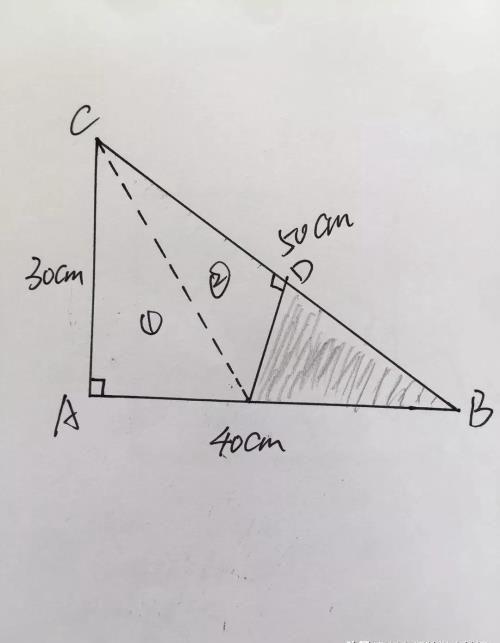
题目：三角形ABC是直角三角形，三边长分别为30cm，40cm和50cm，现沿着虚线折叠使点A恰好落在BC上的点D处，求阴影面积

解答：根据题目给到的条件，沿着虚线折叠使点A恰好落在BC上的点D处，那么①面积等于②面积

又因为阴影部分面积和②号面积等高，所以底的比等于面积比

阴影部分面积：②面积=（50—30）：30=2：3

阴影部分面积：大三角形面积=2：8=1：4

那么阴影部分面积=40×30÷2÷4=150（平方厘米）

这道求阴影部分面积的题是通过等高模型的方法求出的，它很考验小升初学生平时学习中所储备的知识量，如果知识储量够了，这道求阴影面积的题做起来就简单多了，你还能用其他的方法求出这道题阴影部分面积吗？三人行必有我师，期待不同的求解方法，欢迎评论区讨论

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小萱创作整理编辑！