阿氏圆求值方法(阿氏圆求大值)

导语：好题分享——阿氏圆求最值

阿氏圆，又称阿波罗尼斯圆。

已知平面上两点A、B，则所有满足且不等于1的点P的轨迹是一个以定比m：n内分和外分定线段AB的两个分点的连线为直径的圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆。

阿波罗尼斯

运用阿氏圆，可以解决一些初中数学中的“PA+k·PB”型的最值问题。

阿波罗尼斯

当k=1时，即可转化为PA+PB和最小的问题，就是八年级所学的常见的“将军饮马”模型。

但当K不等于1时，再用“将军饮马”模型就无法解决，因此要转换思路：

当P在直线上运动时，即称为“胡不归”问题；（下次再介绍）

当P在圆周上运动时，即称为“阿氏圆”问题。

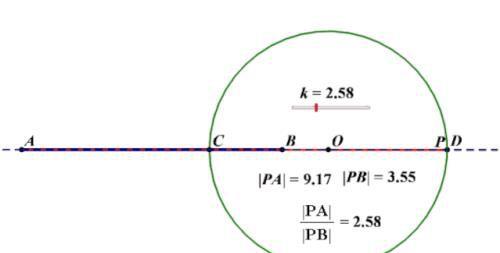
下面以一道例题进行讲解：

如图，在正方形ABCD中，AB=2，E是BC中点，CD上有一动点M，连接EM，BM，将BEM沿着BM翻折得到BFM，连接DF，CF，则DF+FC的最小值是多少？

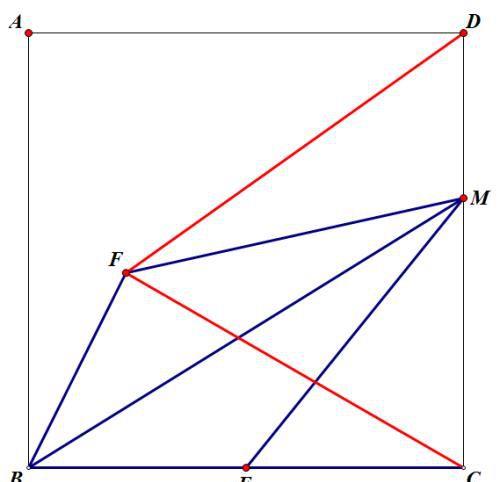
分析题意可得：BE=BF=1，所以F的运动路径是以B为圆心，以1为半径的90度的弧，路径如下图：

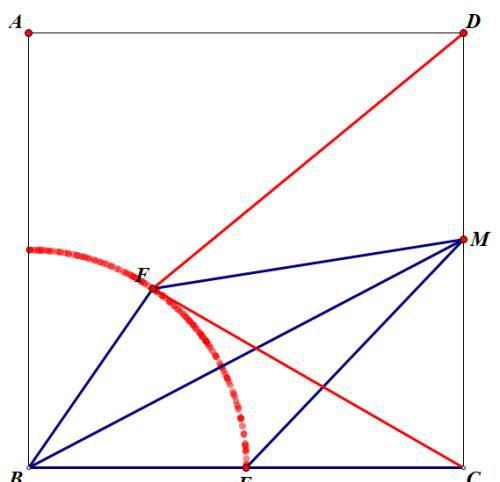
而结论中要求DF+FC的最小值，既使取FC的中点，得到FC，也无法求出DF+FC的最小值。

综合分析可得，F的运动路线是一段弧，且结论符号DF+k·FC的形式，所以需运用阿氏圆求最值的方法。

取BE中点N，使BN=0.5，连接FN

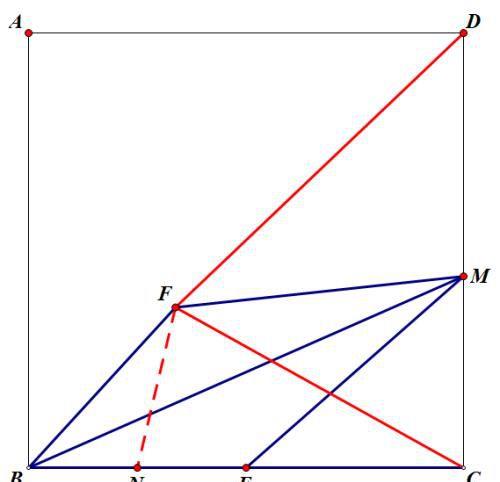
因为，所以BNFBFC，且相似比为1：2，所以，

所以要求DF+FC的最值，即求DF+FN的最小值，

根据“两点之间，线段最短”的结论，可得当D、F、N三点在同一条直线上时，DF+FN有最小值。

由勾股定理可得，DN=

即DF+FC的最小值为。

同学们，你学废了吗？

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！