梯形中间的线段长度怎么求得(梯形中间的线段怎么求)

导语：一道初中几何题-求梯形的内部线段的长

一道初中几何题-求梯形的内部线段的长

在等腰梯形ABCD中， 两个底为AB和CD， 其中AB=500， CD=650， 腰长AD和BC的长为333，∠A和∠D的角平分线相交于点P，∠B和∠C的平分线相交于点Q，求PQ的长度。

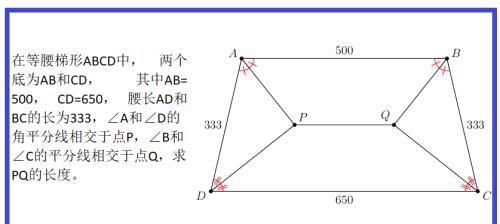
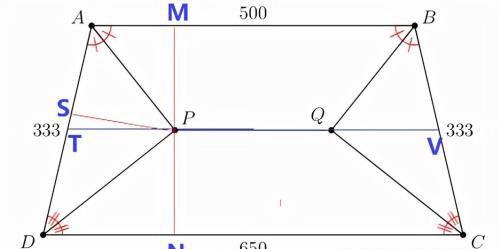
解法1： 如图做辅助线 PM垂直于AB， PN垂直于DC， PS垂直于AD，根据角度平分线的性质， 有PM=PS=PN， 另外AB平行于DC，显然M，P， N三点共线。

由于AB和DC平行，内错角之和为180°，即：

∠DAB+∠ADC=180°，而对应的一半角之和为90°，即：

∠DAP+∠ADP=90°

所以∠APD=180°-90°=90°， PQ的延长线与AD和BC的交点分别是T 和V，

根据P和Q的对称性， 显然PQ平行于DC，且PT=QV

那么PT和QV是直角三角形APD和直角三角形BQC斜边上的中线， 即：

PT=QV=333/2,

T和Q既然是腰的中点，那么TV就是梯形的中线：所以

TV=（500+650）/2=575

最后PQ=TV-PT-QV=575-333/2-333/2=242

解法2： 如图，延长AP和BQ与底边分别相交于W和X，PW he QX 的交点为Z，

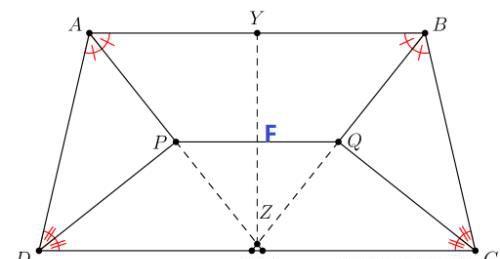
由于DP垂直于AW， 且有AD=AW， 所以DW=333， 同理CX=333

XW=DW+ CX-CD=333+333-650=16,

由于三角形ZXW相似于三角形三角ZBA， 所以：

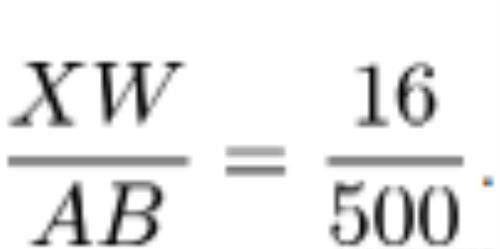
此外三角形ZPQ和三角形ZQB相似， 且PQ为中位线，根据上面的比可以算出两个三角形的高所对应的比可以计算出，首先ZY的高所占的比例份数为：

500

而ZF的高度所占的比例份数为：

(500+16)/2-16=242，

PQ/AB=ZF /ZY

带入上面的比例即：

PQ/500=242/500

PQ=242

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！