初中数学证明边相等的方法(证明边边边)

初中几何中经常会遇到证明边长比例关系的问题。现在总结一下常见的几种方法技巧。以证明三角形角平分线定理为例。

三角形角平分线定理：

在△ABC中，AD是∠BAC的平分线，则AB/BD=AC/CD。

方法1：利用相似三角形的比例关系（相似法）

（这是证明线段长度比例关系最常用的方法）

证明的关键是“构造相似三角形”，“做平行线构造相等角度”是构造相似三角形的最常用方法。

过C作CE∥AB，交AD的延长线于E

∵CE∥AB

∴∠ABC=∠BCE，且∠BAD=∠AEC（平行线形成的内错角相等）

∴△ABD∽△ECD

∴AB/EC=BD/DC

∵AE是∠BAC的角平分线

∴∠CAE=∠CEA，即△ACE是等腰三角形，AC=EC

于是得到：AB/AC=BD/DC。证毕。

方法2：利用图形面积的比例关系证明线段的比例关系（面积法）

（很多看似复杂不知该如何构造相似三角形的问题可以尝试）

在△ABC中，AD是∠BAC的平分线

过点D作DE⊥AB，DF⊥AC

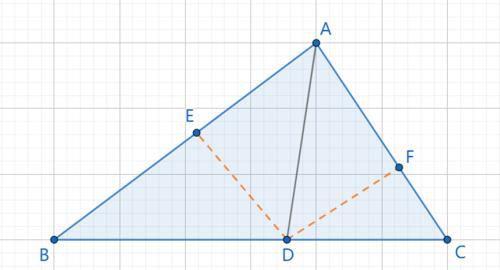
∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC

∴DE=DF

∵2S△ABD=AB×DE且2S△ACD=AC×DF

∴S△ABD：S△ACD=AB：AC

又∵S△ABD：S△ACD=BD：CD（同高，面积比例为底边比例）

∴S△ABD:S△ACD=AB：AC=BD:CD

∴AB:AC=BD:CD

方法3：代数法（利用正弦定理、余弦定理计算边长的数量关系）

正弦定理：△ABC中，∠A、∠B、∠C对边分别为 a、b、c。

则有a/sinA=b/sinB=c/sinC=2R（R为三角形外接圆半径）

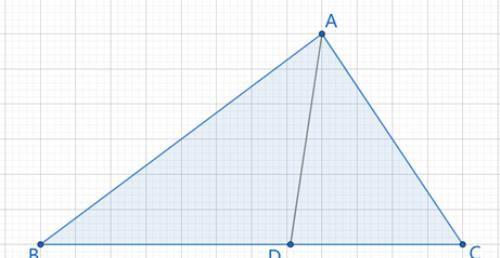
根据正弦定理有：

AB/BD=sin∠ADB/sin∠BAD

AC/CD=sin∠ADC/sin∠CAD

∵∠ADB与∠ADC互为补角

∴sin∠ADB= sin∠ADC

∵AD为∠BAC的平分线

∴sin∠BAD= sin∠CAD

∴AB/BD= AC/CD，即AB/AC=BD/CD

以上是总结的几种证明边长比例关系的常用方法。在遇到类似问题时，脑海中应当迅速地遍历一下这几种方法并进行心算推演，一定会大大提升解题效率。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小快创作整理编辑！