求面积辅助线(初中数学几何经典模型及辅助线做法)
中考几何进阶 10 辅助线法则(10)面积模型
相似模型
所有面积模型的根,是相似三角形定理:相似三角形面积比等于相似比的平方。
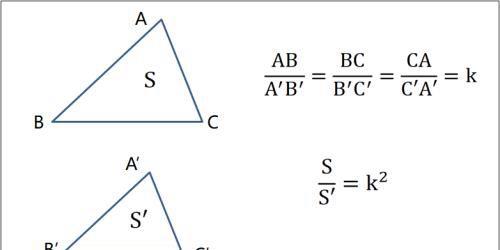
------------
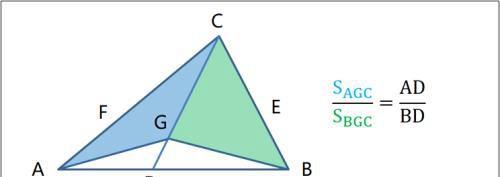
等积模型(三角形)
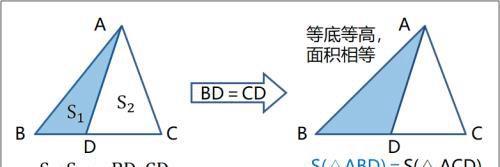
------------
等积模型(三角形)
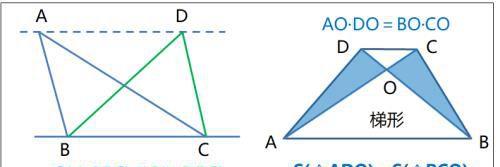
相交于O点的线段AC、BD满足AO·DO=BO·CO的充分必要条件是ABCD(AB∥CD)为梯形。
------------
等积模型(平行四边形)
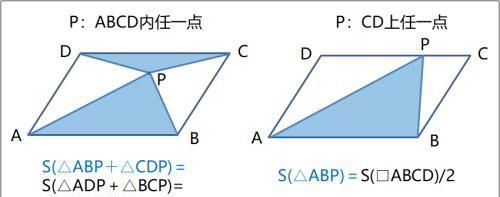
------------
等积模型(任意四边形)
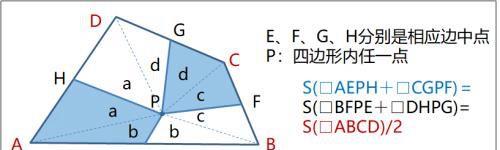
------------
蝴蝶定理模型(任意四边形)
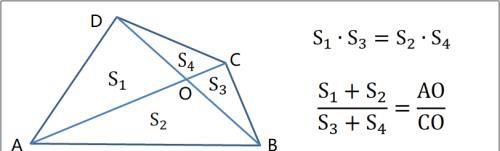
------------
等角模型
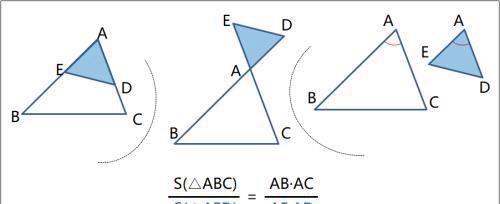
------------
补角模型
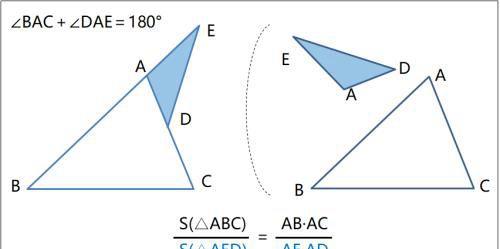
------------
燕尾模型
------------
例题 如图,正方形ABCD的面积是8,CEFG为正方形,求阴影部分的面积。
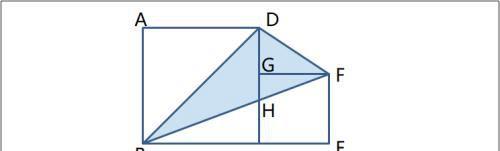
〖分析〗
涉及到求面积,典型辅助线一般有平行线、三角形中线、角平分线、和面积割补相关的线段等。
由题设,BD已知,基本出发点是 三角形面积=底×高÷2。过F作BD边的高h,这个高 直接求很难。但别忘了我们要求的是阴影的面积,可以看看能不能找到同底等高的三角形,为此过F作平行于BD的直线,易知恰好过点C。
连接FC,易知FC∥BD,△BFD与△BCD同底等高,
∴S(△BFD)=S(△BCD)=S(□ABCD)/2=4。
------------
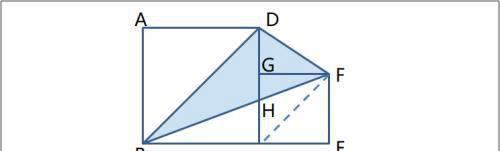
例题 已知长方形ABCD被AF、BE分为四块,已知各块面积如图,求阴影面积。
〖分析〗
欲求阴影面积,实则求出长方形ABCD面积即可。根据平行四边形等积模型, S(□ABCD) =2×S(△ABE)。问题转化为求S(△AOE)。
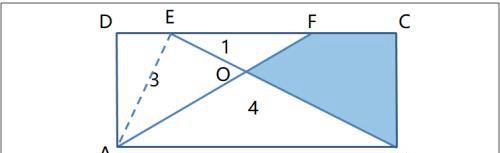
在△ABE中:S(△AOE)∶S(△AOB)=EO∶BO=k,但k是相似三角形△EOF和△AOB的相似比:
k^2=S(△EOF)∶S(△AOB)=1∶4,∴k=0.5,
即:S(△AOE)∶S(△AOB)=0.5,∴S(△AOE)=0.5×S(△AOB)=2;
S(□ABCD) =2×S(△ABE)= 2×[S(△AOE)+S(△AOB)]=12;
阴影面积=S(□ABCD)-S(△EOF)-S(□AOED)-S(△AOB)=4。
------------
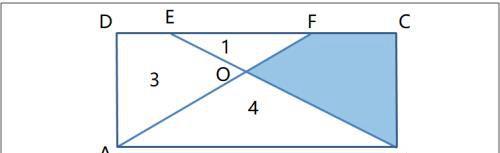
例题 如图长方形ABCD,②号面积为4, ⑤号面积为5,求阴影面积。
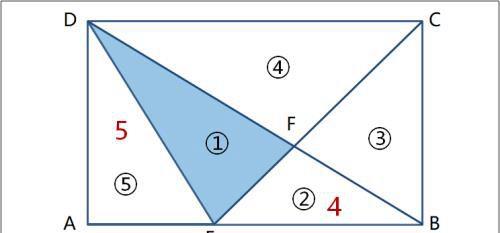
〖分析〗
根据平行四边形等积模型,
S(①+④)=S(①+②+⑤)=S(□ABCE)÷2
∴S(④)=S(②+⑤)=9;
再根据梯形等积模型,S(①)=S(③);
再由四边形蝴蝶定理:S(①)×S(③)=S(②)×S(④)=36,
解得S(①)=S(③) =6。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小莉创作整理编辑!