祖冲之的圆周率是怎样计算出来的(祖冲之在圆周率计算上有哪两项成果)
祖冲之是我国南北朝时期著名的数学家、天文学家。他在数学上面有个重要贡献就是圆周率,他推算出了圆周率的真值,介于小数点的后第七位。
精准度那么高的圆周率,即使用算盘完成这些计算,也不是一件轻而易举的事。试想当时的祖冲之每天只用纸笔,一次次的推算检验,日复一日地重复着这种状态,这是一件多么艰辛的事情,得需要多大的毅力。

那么祖冲之是怎么算出精度这么高的圆周率的呢?他的成就是建立在刘徽的割圆术基础之上的,他并不满足于验证前人的结论,而是加以发展,获得了超越前人的重大成就。
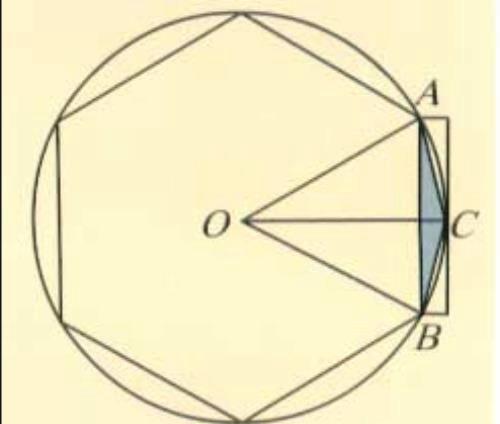
祖冲之按照刘徽的割圆术,刘徽的割圆术基于圆的内接正多边形,他用正多边形的面积来逼近圆的面积。分割越多,内接正多边形和圆之间的面积越来越小,两者越来接近。无限分割之后,内接正多边形和圆将会合二为一。祖冲之设了一个直径为一丈的圆,在圆内切割计算。当他切割到圆的内接一百九十二边形时,得到了的数值。他继续切割,作了三百八十四边形、七百六十八边形……直到他切割到二万四千五百七十六边形,祖冲之依次求出每个内接正多边形的边长。最后求得直径为一丈的圆,它的圆周长度在三丈一尺四寸一分五厘九毫二秒七忽到三丈一尺四寸一分五厘九毫二秒六忽之间。换句话说:如果圆的直径为1,那么圆周小于3.1415927、大大不到千万分之一,它们的提出,大大方便了计算和实际应用。
我们可以想象,在祖冲之那个朝代,要作出这样精密的计算,是一项极为细致且艰巨的脑力劳动,甚至算是一项不可能完成的任务。
祖冲之就用一根根小棍子进行运算,圆周率的数值,需要进行复杂的加、减、乘、除和开方运算,而每个步骤都要反复进行十几次,开方运算有50次。一有差错,比如计算中出现了错误,就只能从头开始。要求得祖冲之圆周率的数值,就需要对九位有的小数进行15927加、减、乘、除和开方运算等十多个步骤的计算,而每个步骤都要反复进行十几次,开方运算有50次,最后计算出的数字达到小数点后十六、七位。

不过祖冲之成功了,他计算出来的圆周率被称为,延续800年,一直到现在还在用。所以,祖冲之在圆周率方面的研究,有着积极的现实意义,真的是了不起。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小娴创作整理编辑!