二次函数倍角问题压轴题(二次函数中二倍角问题)

导语：中考压轴：二次函数中的倍角问题方法总结(二)

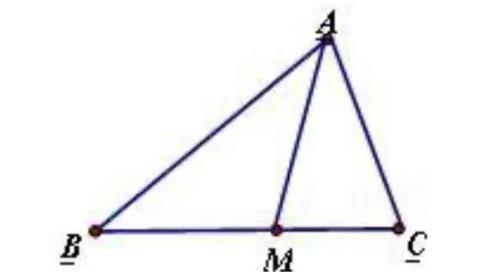
例：(1)如图，三角形ABC中，AM平分∠BAC，求证:BM/CM=AB/CA

分析：过点B作BD∥AC，交AM延长线于点D

易证：△BMD～△CMA

∴BM/CM=BD/CA

∵BD∥AC，AM平分∠BAC

∴∠1=∠2=∠3

∴AB=BD

即：BM/CM=AB/CA。(多种方法可证明)

(2)探索:如图已知二次函数y=−3/4x²+9/4x+3，与x轴交与A，B两点，与y轴交与C点，点P是抛物线第三象限上动点，若∠PBA=1/2∠BCO，求点P的坐标

方法一：加倍法构造等角，结合(1)问结论，求出BD解析式，联立求出点P坐标。

分析：作∠PBE=∠PBA交y轴于点E

则∠EBO=∠BCO

易求：B(4，0)，C(0，3)

∴OB=4，OC=3，BC=5

∵∠EBO=∠BCO

∴△EBO～△BCO

由相似⇒BE=20/3，OE=16/3

∵BD平分∠EBO，由(1)问得：

OD/DE=OB/BE=4:20/3

∴OD/DE=3:5

即：OD=3/8.OE=2，

∴D(0，−2)

求出BD解析式：y=1/2x−2①

y=−3/4x²+9/4x+3②

①②联立得：x₁=4，x₂=−5/3

∴P(−5/3，−17/6) 。

方法二：减半法构造等腰三角形，可不用(1)问结论

分析：延长OC至点E，使CE=BC=5

则：∠OBD=∠1=∠2=1/2∠BCO

OE=8

∴△OBD～△OEB

由相似⇒OD=2

∴D(0，−2)

求出BD解析式：y=1/2x−2①

y=−3/4x²+9/4x+3②

①②联立得：x₁=4，x₂=−5/3

∴P(−5/3，−17/6) 。

方法三：减半法构造等角，结合(1)问结论，求出BD解析式，联立求出点P坐标。

分析：作∠BCO的角平分线CE，交OB于点E

则∠1=∠2=∠3

由(1)问得：OE/BE=OC/BC=3:5

∴OE=3/8.OB=3/2

易证：△OBD～△OCE

由相似⇒OD=2

∴D(0，−2)

求出BD解析式：y=1/2x−2①

y=−3/4x²+9/4x+3②

①②联立得：x₁=4，x₂=−5/3

∴P(−5/3，−17/6) 。

本文内容由小洁整理编辑！