高中数学函数求值常用方法总结图(高中数学函数求值常用方法总结怎么写)
导语:高中数学函数求最值常用方法总结
高中数学中的函数最值求解问题是学习中的难点,在解决函数最值问题的时候要经过全方位的考虑,结合函数的定义域,将各种可能出现的结果进行分析,最终求得准确的计算结果。
在数学学习的过程中活跃的数学思维非常重要,它不仅可以改善学习方法,而且可以帮助学生掌握更多的解题技巧,进而提高解题速度和学习效率。
本文总结了一些求函数最值的常用方法如下:
一、利用一次函数的单调性
【例题1】已知 x , y , z 是非负实数,且 x + 3y + 2z = 3 , 3x + 3y + z = 4 ,
求函数 w = 2x - 3y + z 的最值 .
解:
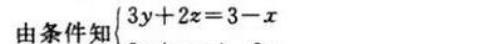
得 y = 5/3(1 - x), z = 2x - 1
∴ w = 9x - 6
又 x , y , z 非负,

依一次函数 w = 9z - 6 的单调性可知
当 x = 1/2 时,Wmin = -3/2 ,
当 x= 1 时,Wmax = 3 .
注:
再求多元函数的条件最值时,通常是根据已知条件消元,转化为一元函数来解决问题.
对于一次函数 y = kx + b ( k ≠ 0 ) 的最值,关键是指出自变量的取值范围,即函数的定义域,当一次函数的定义域是闭区间时,其最值在闭区间的端点处取得 .
二、利用二次函数的性质
【例题2】设 α , β 是方程 4x^2 - 4kx + k + 2 = 0 的两个实数根,
当 k 为何值时 α^2 + β^2 有最小值?
解:
∵ α , β 为方程的两个实数根,
∴ α + β = k , αβ = 1/4 ( k + 2 ) ,
令 y = α^2 + β^2 , 则有
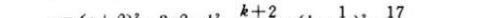
又由原方程由实数根可知,

∴ k ≤ -1 或 k ≥ 2 .
而二次函数的顶点 (1/4,-17/16)不在此范围内,根据二次函数的性质知,
y 是以 k = 1/4 为对称轴,开口向上的,定义域为 (-∞,-1]∪[2,+∞)的抛物线,
比较 k = -1 及 k = 2 时 y 的值知,
当 k = -1 时,有 ymin = 1/2 .
注:
利用二次函数的性质求最值时,不能机械地套用最值在顶点处取得 . 首先要求出函数的定义域,然后在看顶点是否在函数的定义域内,最后再根据函数的单调性来判定 .
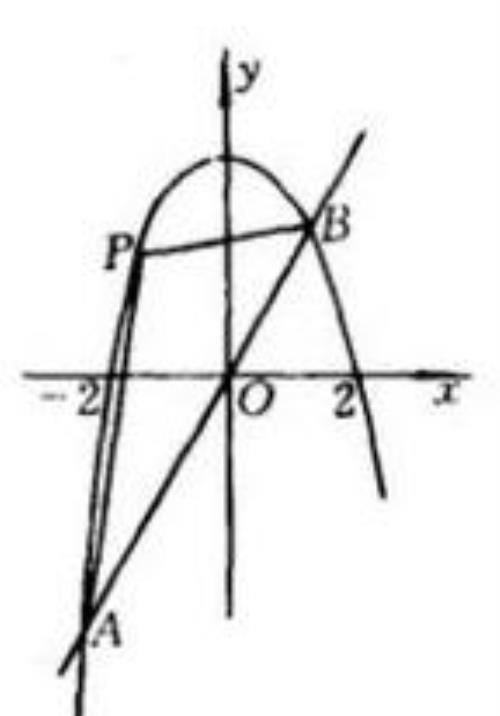
【例题3】如图所示,抛物线 y = 4 - x^2 与直线 y = 3x 交于 A , B 两点,
点 P 在抛物线上由 A 运动到 B,求 △APB 的面积最大时点 P 的坐标 .
分析:
由于 A , B 为定点,所以 AB 长为定值,欲使 △APB 的面积最大,须使 P 到 AB 的距离最大 .
解:
设 P 点坐标为 (x0 , y0),
∵ A , B 在直线 y = 3x 上,
∴
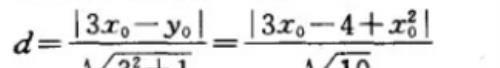
联立抛物线与直线方程,可得
xA = -4 , xB = 1 ,
∴ -4 ≤ x0 ≤ 1 ,
则有
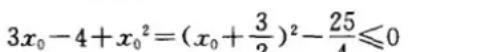
∴
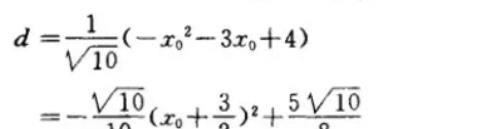
当 x = -3/2 时,d 取最大值,△APB 面积最大,此时 P 点坐标为 (-3/2 , 7/4).
注:
在解决实际问题时要注意确定自变量取值范围的方法,本题是由直线与抛物线的交点来确定的,这样才能确定定义域内的最值 .
三、利用二次方程的判别式
欲求函数 y = f(x) ( x ∈ R ) 的极值,如果可以把函数式整理成关于 x 的二次方程,
注意到 x 在其定义域内取值,即方程有实根,
所以可以通过二次方程的判别式 △ ≥ 0 来探求 y 的极大值与极小值 .
【例题4】已知 0 ≤ x ≤ 1 , 求
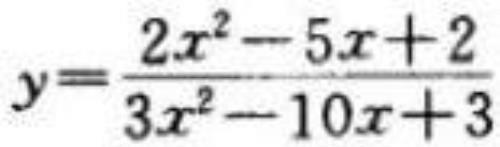
的最值 .
解:原式可化为

∵ x ∈ R ,
∴

解得 y ≤ 1/4 或 y ≥ 9/16 ,
即函数 y 的值域为 y ≤ 1/4 或 y ≥ 9/16 ,
∴ y极大 = 1/4,y极小 = 9/16 .
当 y = 1/4 时,代入原函数解析式得 x = 1 ∈ [ 0 , 1 ] ;
当 y = 9/16 时,代入原函数解析式得 x = -1 ∉ [ 0 , 1 ] .
又 x = 0 时 , y = 2/3 ,
∴ 当 x = 0 时,y 取极大值 2/3 .
注:
① 由判别式确定的是函数的值域,由值域得到的是函数的极值而不是最值;
② 对有些函数来说,极值与最值相同,而有的函数就不一定,
如本题中的极大值比极小值还小,这是因为极值是就某局部而言;
③ 若要求函数在给定的定义域内的最值,一定要注意极值是否在此定义域内取得,
即要注意验根 .
四、利用重要不等式
【例题5】设 x , y , z ∈ R+ , 且 2x + 4y + 9z = 16 .
求 6√x + 4√y + 3√z 的最大值 .
解:
令 u = 6√x + 4√y + 3√z ,
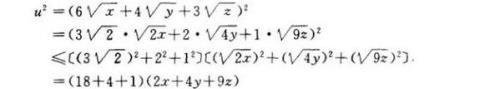
∴ u ≤ 4√23 ,
( 其中当 9/x = 1/y = 1/9z 时,即当 x = 144/23 , y = 16/23 , z = 16/207 时取等号)
故

注:
这里是应用柯西不等式,在应用公式时,
如何构造出已知条件等式 2x + 4y + 9z = 16,颇具技巧性和解题意义 .
五、利用三角函数的有界性
对于三角函数的极值,通常是利用三角函数的有界性来求解问题的,
如正、余弦函数的最大(小)值很明显:y = asinx + bcosx (a , b ≠ 0)
引入辅助角 θ,则
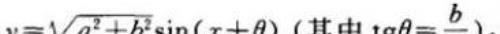
其最值也一目了然 . 而对于其它的类型或用同角关系式、或用万能公式、或用正余弦定理作转化,变为二次函数问题来求解 .
【例题6】求
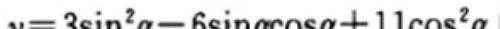
的最值 .
解法一:(利用降幂公式)
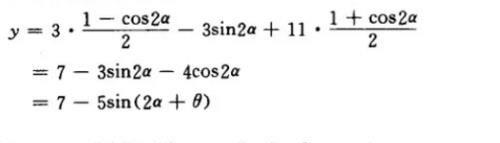
解法二:(用判别式法)

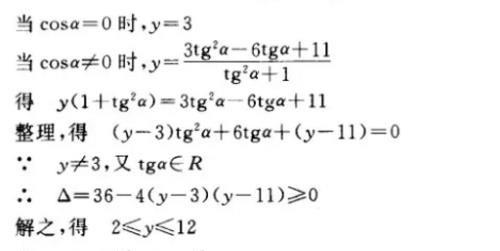
注:本例还可以用万能公式等方法来求解 .
六、利用参数换元
对于有些函数而言,直接求极值比较复杂或不方便,这时可根据题目的特点作变量代换,然后运用前面的几种方法来解决问题.在换元时,一定要注意新的变量的取值范围 .
【例题7】求函数 y = x + √( 1 - x ) 的极值 .
解:

原函数变为
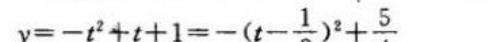
∵ t = 1/2 ∈ [ 0 , +∞ ) ,
∴ 当 t = 1/2 ,即 x = 3/4 时,ymax = 5/4 .
注:这种换元虽然十分简单,但具有代表性 .
七、利用复数的性质
【例题8】已知复数 z 满足 | z | = 2 , 求 | 1 + √3 i + z | 的极值 .
解法一:
设 z = 2(cosθ + isinθ) (∵ | z | = 2)
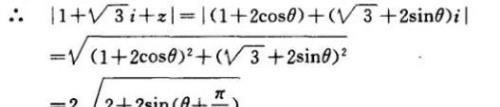
故 | 1 + √3 i + z |max = 4 , | 1 + √3 i + z |min = 0 .
解法二:
依据 | z1 | - | z2 | ≤ | z1 + z2 | ≤ | z1 | + | z2 | ,
有 | 1 + √3 i | - | z | ≤ | 1 + √3 i + z | ≤ | 1 + √3 i | + | z | ,
即 2 - 2 ≤ | 1 + √3 i + z | ≤ 2 + 2 ,
∴ | 1 + √3 i + z |max = 4 , | 1 + √3 i + z |min = 0 .
注:
求复数模的最值通常可用代数法,三角法(解法一),
复数模的性质及其公式 | z1 | - | z2 | ≤ | z1 + z2 | ≤ | z1 | + | z2 | ,
此外还有数形结合方法等,但以上两种方法最为简捷.
八、利用数形结合
有些代数和三角问题,若能借助其几何背景,予以几何直观,这时求其最值常能收到直观、明快,化难为易得功效.
【例题9】求
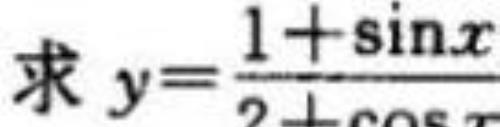
的最值 .
解:将函数式变形为
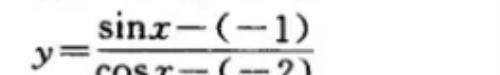
其几何意义是在直角坐标系中,动点 P(cosx , sinx)和定点 A(-2 , -1)连线的斜率,
动点 P 的轨迹为单位圆,如下图所示:
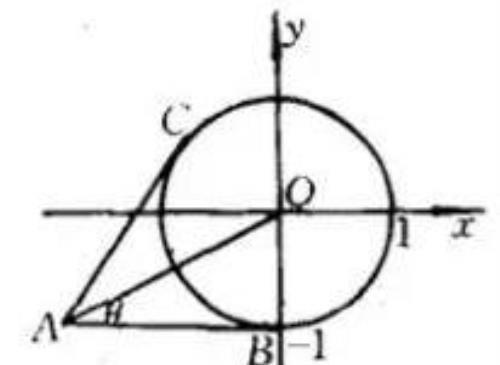
知 kAB 最小,kAC 最大,显然 kAB = 0 ,
又 tgθ = |OB|/|AB| = 1/2 ,
tg∠A = tg2θ = 2tgθ/(1 - tg^2 θ)= 4/3 ,
即 kAC = 4/3 ,
故 ymin = 0 , ymax = 4/3 .
注:
形如 [f(x) - a] / [g(x) - b] 的函数式,
通常都可视作点 (g(x) ,f(x) ) 与点 (b , a)的连线的斜率 .
运用数形结合的思想解题,关键是要进行合理的联想和类比,
将代数式通过转化、变形、给予几何解释,
通常这种转化与变形的过程常是一种挖掘和发现的过程,如本例需要挖掘 .
高中数学100个知识点总结!
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小楠创作整理编辑!