公切线导数问题(导数公切线方程怎么求)

导语：导数的一题多解 公切线的引入

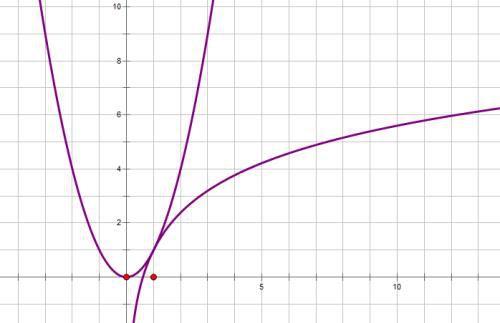
函数f(x)=x^2,g(x)=2lnx+a有公共点，则a的取值范围是（ ）

A（e,+ꚙ) B (1.+ꚙ) C[1,+ꚙ) D(-ꚙ,1)

解法一：

数形结合

由图可知，（1，1）相切，此时只有一个公共点，如果有交点的话，lnx+a只能向上平移，故a≥1

解法二：

转化法：

转化函数为h(x)=f(x)-g(x)=x^2-2lnx-a有零点，通过求导判定其单调性，其最小值是小于等于0

解法三：分离参数法：

转化a=x^2-2lnx有解，即函数y=a和函数y=x^2-2lnx有交点，故选C

解法四：

由于题目告知公共点，即告诉我们至少一个交点，即切点

即求他们的公切线。

f(x)=x^2的切线斜率2x0

g(x)=2lnx+a 的切线斜率2/x0

即他们的斜率相等，x0=1,得出a=1

且x^2抛物线在上，所以2lnx+a继续有交点只能向上平移。所以a≥1

在导数的初期基础学习中，引入导数的概念也是通过切线直观感受得出的，所以有时候我们需要在学习中追本溯源。

本文内容由小畅整理编辑！