从一个高考题看看数学里的对称性是什么(从一个高考题看看数学里的对称性是否正确)

导语：从一个高考题看看数学里的对称性

这是从条友那里看到的一个数学高考题，解法是我自己给的。

如题：已知函数 f(x) = e^x - ax 和 g(x) = ax - lnx 有相同的最小值，

1）求 a，

2）证明：存在直线 y = b 与两条曲线 y = f(x) 和 y = g(x) 共有3个不同的交点，并且从左到右3个交点的横坐标成等差数列。

1，首先看 y = e^x 和 y = lnx 这两个函数。

y = lnx 就是 x = e^y，它与y = e^x是对称的：

如果(x, y) 是曲线 y = e^x上的点，

那么交换横纵坐标之后，(y, x) 就是曲线 y = lnx上的点（或者 x = e^y）。

这两点确定的直线的斜率是：(x - y) / (y - x) = -1.

它们的对称轴应该垂直于它们确定的直线，所以对称轴的斜率是1。

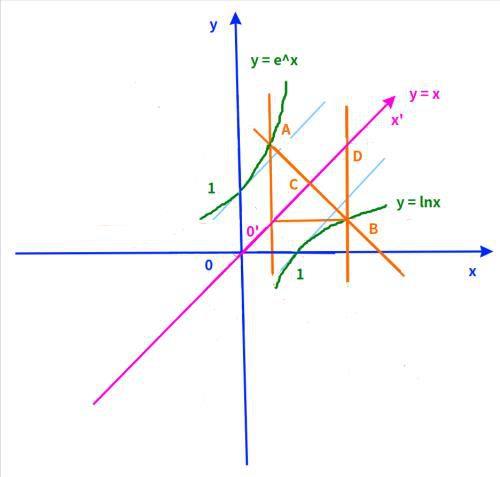
假设它们确定的直线与对称轴的交点是(x0, x0)，那么：

点(x, y) 到交点的距离的平方是：(x - x0)^2 + (y - x0)^2，

点(y, x) 到交点的距离的平方是：(y - x0)^2 + (x - x0)^2，

所以它们到交点的距离是相等的，也就是说交点在直线 y = x上：这就是对称轴，也是两点连线的垂直平分线。

所以，a = 1。

同时可得，AC = BC，AO&39; = BD，

因为这些夹角要么是90度，要么是45度，三角形ACO&39; = e^x - x = f(x)，BD = x - lnx = g(x)，它们是相等的。

也就是说，在关于 y = x的对称下，f(x) 和 g(x) 的值是相等的。

当这两点AB之间的距离最小时，f(x) 和 g(x) 同时取得最小值，因为：

但是当它们取得最小值时，f(x) 和 g(x) 对应的x坐标不一样。

f(x) = e^x - x 的导数是 e^x - 1 = 0，对应的坐标：x = 0，y = 1。

g(x) = x - lnx 的导数是 1 - 1/x = 0，对应的坐标：x = 1, y = 1。

二阶导数分别是e^x 和 1/x^2 都 > 0，所以它们两个的极值都是极小值。

在x趋向于正无穷大的时候，f(x) 和 g(x) 也趋向于正无穷大。

同时，g(x)在x趋向于0的时候，还是趋向于正无穷大。

所以，f(x) 和 g(x) 在0和1之间有一个交点（微分中值定理）。

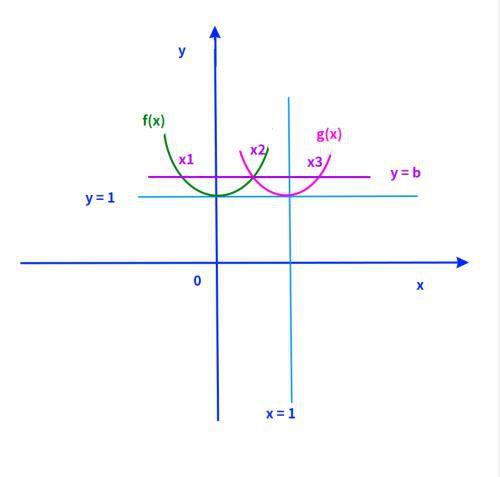
从这个交点做一条水平线，与 f(x)和g(x)的交点就是3个。

如果它们成等差数列，那么x2 - x1 = x3 - x2.

等差数列的证明：

f(x) 和 g(x) 是关于y = x对称的，所以把它旋转45度、再把坐标中心移动到(1/2, 1/2)，看起来最顺眼[呲牙]

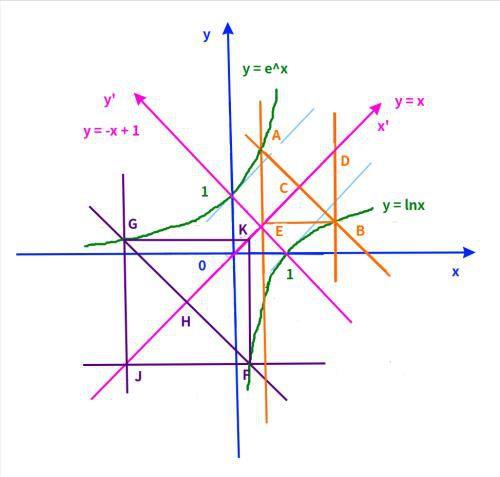
如上图，关于y = x对称的两点FG，也可以得出GJ = FK = FJ = GK，

跟AB得出的AE = BD = BE 一样。

因为(0,1)和(1,0)的连线是最小值，而两边都趋向于无穷大，所以可以找到一点，满足：

f(x) = GJ = FK = AE = BD = g(x)，

这时两点EK重合，AE(K)F 三点共线。

EK重合的那点，就是f(x)和g(x) 在区间(0, 1)上的交点：

这时GK和BE是相等的，K和E是重合的，也就是三个点的x坐标是等差数列。

在x趋向于0的时候，e^x - x < x - lnx，

在x趋向于1的时候，e^x - x > x - lnx，因为e - 1 > 1，

所以，在(0, 1)之间总有一点让 e^x - x = x - lnx，即f(x) = g(x).

（这算是微分中值定理，还是算夹挤准则？）

然后，根据 f(x) 和 g(x) 关于 y = x的对称性，就可以得出：

1，GJ = FK = AE = BD，即2条曲线、3个交点的y坐标相等，

2，GK = FK = AE = BE，即3个交点的x坐标是等差数列。

现在把微积分压到高中了，还好没把实变压到高中里[捂脸]

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！