交变电场是什么意思(交变电场中几种典型问题)
导语:一轮复习:交变电场
交变电场是指电场强度为交变量的电场(即电场强度、通断都随时间改变的电场)。
一、常见的交变电场:
产生交变电场的电压波形有方形波、锯齿波、正弦波等
二、常见的运动情况
(1)单向(往复)直线运动(平行电场方向进入)
(2)偏转运动(垂直电场方向进入,类平抛运动)
三、处理方法
1画粒子运动的v-t图
①直线运动的直接画v-t图
②曲线运动的画单方向v-t图
☞不管从什么时刻进入的,从t=0时刻开始画起,然后移动坐标系到开始进入时刻。
2画轨迹图
☞从开始进入时画轨迹图,后分段截取,画图要充分利用对称性。
3数学分析法
四、注意
1时间周期性
2空间对称性
3边界条件
4对于锯齿波和正弦波等电压产生的交变电场,带电粒子穿过电场的时间内可认为电场不变(如有关示波器的计算)
类型一:带电粒子在交变电场中做直线运动
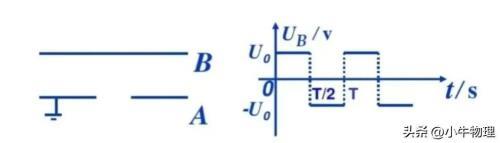
示例一:如图所示,
A板的电势U=0,B板的电势U随时间的变化规律如图所示。则()
A.若电子是在t=0时刻从A板小孔进入的,它将直向B板运动
B.若电子是在t=T/8时刻进入的,它可能时而向B板运动,时而向A板运动,最后打在B板上
C.若电子是在t=3T/8时刻进入的,它可能时而向B板运动,时而向A板运动最后打在B板上
D.若电子是在t=T/2时刻进入的,它可能时而向B板、时而向A板运动
【解析】
首先把U-t图转化为v-t图
具体转化过程:
E=U/d
a=qE/m
从T/8时刻进入的,就把坐标系移到T/8时刻。
从T/4时刻进入的,就把坐标系移到T/4时刻。
从3T/8时刻进入的,就把坐标系移到3T/8时刻。
例题:如图所示,A、B是一对中间开有小孔的平行金属板,两小孔的连线与金属板垂直,两极板间的距离为。在两极板间加上低频交流电压,当A板电势为零时,B板电势U=U₀cosωt。现有一电子(质量为m,电荷量为e)在t=0时刻穿过A板上的小孔射人电场,设电子的初速度和重力均可忽略不计,分析电子在两极板间可能的运动情况。
类型二:带电粒子在交变电场中偏转
示例二:如图甲所示,两平行金属板水平放置,间距为d,金属板长为L=2d,两金属板间加如图乙所示的电压(初始时上金属板带正电),其中U₀=16md²/qT²,一粒子源连续发射质量为m、电荷量为+q的带电粒子(初速度v₀=4d/T,重力忽略不计),射出的带电粒子恰好从上金属板左端的下边缘水平进入两金属板间。
(1)求能从板间飞出的粒子在板间运动的时间。
(2)在哪些时刻进入两金属板间的带电粒子不碰到金属板而能够飞出两金属板间?
【解析】
(1)水平方向做匀速直线运动,t=L/v₀=T/2
(2)只要能飞出电场,时间长度一定为½T,加速度a=qU₀/md=16d/T²。
方法一:纯数学分析法
设加速度向下的时间为t,则加速度向上的时间为½T-t(因为总时间为½T,加速度向下或者向上只出现一次),要从极板飞出,竖直位移要大于等于0而小于等于d,列式为
0≤½at²+[at·(½T-t)-½a(½T-t)²]≤d
取临界解得:舍去不合理值,
t≤¼T且t≥¼(2-√2)T,
进入时间为t₁≥½T-¼T=¼T,
t₂≤½T-¼(2-√2)T=¼√2T
结合两种情形向进行分析,进入时刻考虑到周期性,带电粒子不碰到金属板而能够飞出两金属板间的时刻T₀满足(¼+n)T≤T₀≤(¼√2+n)T(其中n=0,l,2,…)
方法二:v-t图分析法
用竖直方向上的Vy-t图进行分析,取向下为正方向,先不管从什么时刻进入的,都从0时刻进入开始分析,画出Vy-t图,如图所示,
若从0时刻进入,时长为½T,竖直向下的位移为2d,将打在下极板上,不合题意,进入时刻必须往后推移,将坐标系往右平移,进入时刻在¼T,面积恰好为d,计算过程为2×½a(¼T)²=d,则进入时刻为t₁=¼T,如图所示,
接着往右平移坐标系一小段,注意时间长要保持½T,将会出现负面积,此时正面积还是大于负面积,总面积<d,能出电场,符合题意,如图所示,
继续向右平移坐标系,当负面积和正面积相等时,即竖直位移为零,也就是刚好从上极板右端飞出,如图所示,
设加速度向下的时间为t,则加速度向上的时间为½T-t
2×½at²=½a(½T-2t)²
解得t=¼(2+2√2)T
则进入时刻t₂=½T-t,t₂=¼√2T
结合两种情形向进行分析,进入时刻考虑到周期性,带电粒子不碰到金属板而能够飞出两金属板间的时刻T₀满足(¼+n)T≤T₀≤(¼√2+n)T(其中n=0,l,2,…)
方法三:轨迹图法
交变电场往往具有周期规律性,用画轨迹的方法关键是找到对称性。
0时刻进入的将打在下极板上,如图线①所示,不合题意,因此进入时刻必须推后,轨迹将会出现拐点,如图线②所示,直至恰好从下极板右端飞出,进入时刻继续推后,拐点往左移动,并且还会出现竖直速度为0的另一拐点(对称性),轨迹将往上偏移,直至恰好从上极板右端飞出。如图线③所示。
恰好从下极板右端飞出,速度水平且为v₀,由对称性,显然可知粒子在电场中运动时间为¼T,进入时刻为t₁=½T-¼T=¼T。
恰好从上极板右端飞出,在第一个半个周期内,设带电粒子在t₂时刻进入两金属板间,它在竖直方向上先加速向下,经过t时间后电场反向,开始在竖直方向上减速向下,又经过时间t,竖直分速度减为零,然后加速向上,经过时间½T-2t直到恰好从上金属板右端飞出,画出其运动轨迹,如图所示。
找到电场方向相反的两个对称时间,这样竖直速度就会为零。
从右端飞出,竖直位移为零
2×½at²=½a(½T-2t)²
解得t=¼(2+2√2)T
则t₂=½T-t=¼√2T
结合两种情形向进行分析,进入时刻考虑到周期性,带电粒子不碰到金属板而能够飞出两金属板间的时刻t满足(¼+n)T≤T₀≤(√2/4+n)T(其中n=0,1,2,…)
例题:如图甲所示,电子以水平初速度v₀沿平行金属板中央射入,在金属板间加上如图乙所示的交变电压.已知电子质量为m,电荷量为e,电压周期为T,电压为U₀,
求:
①若电子在t=0时刻进入板间,在半周期内恰好能从板的上边缘飞出,则电子飞出速度多大.
②若电子在t=0时刻进入板间,能从板右边水平飞出,则金属板多长.
③若电子能从板右边O′水平飞出,电子应从哪一时刻进入板间,两板间距至少多大.
例题:如图甲所示,长为8d、间距为d的平行金属板水平放置,点有一粒子源,能持续水平向右发射初速度为v₀、电荷量为q(q>0)、质量为m的粒子.在两板间存在如图乙所示的交变电场,取竖直向下为正方向,不计粒子重力.以下判断正确的是(AD)
例题:如图甲所示,真空中两水平放置的平行金属板A、B相距为d,板长为L,今在A、B两板间加一如图乙所示的周期性变化的交变电压.从t=0时刻开始,一束初速度均为v₀的电子流沿A、B两板间的中线从左端连续不断地水平射人板间的电场,要想使电子束都能从A、B右端水平射出,则所加交变电压的周期T和所加电压的大小应满足什么条件?
类型三:锯齿电压、正弦电压
每个电子穿过平行板电容器的时间都极短,可以认为电压是不变的,电场变中不变,这其实是一种近视处理的方法。在示波器这类问题中必须理解这种方法。
具体的含义就是:粒子是t₁时刻进入电场的,则粒子穿过电场的过程中,电场强度一直保持E₁不变;粒子是t₂时刻进入电场的,则粒子穿过电场的过程中,电场强度一直保持E₂不变。
什么时刻开始进入电场的,在穿过电场的整个过程中,一直保持该时刻的电场不变。
示三例:如图甲所示,
热电子由阴极飞出时的初速度忽略不计,电子发射装置的加速电压为U₀,电容器板长和板间距离均为L=10cm,下极板接地,电容器右端到荧光屏的距离也是L=10cm,在电容器两极板间接一交变电压,上、下极板间的电势差随时间变化的图象如图乙所示.(每个电子穿过平行板电容器的时间都极短,可以认为电压是不变的)
(1)在t=0.06s时刻发射电子,电子打在荧光屏上的何处?
(2)荧光屏上有电子打到的区间有多长?
☞在t=0.06s时刻发射电子,电场强度取t=0.06s时刻的,即1.8U₀并且在粒子运动过程中保持这个电压不变。
本文内容由快快网络小林整理编辑!