图形的翻折变换(中考数学图形的翻折问题)

导语：中考数学图形变换之翻折变换

一、翻折变换

指把某个图形按照给定的条件折叠，通过折叠前后图形变换的相互关系来命制的一类问题；

也指解题时需要借助轴对称变换构造辅助线来帮助问题获得解决的一类问题．

这类题主要考查考生的识图能力、动手操作能力、灵活运用知识解决问题的能力等．

二、主要题型

①以翻折变换为载体的问题；

②利用轴对称变换为工具解题．

三、解题方法

①以翻折变换为载体的问题，考查几何图形的判定和性质的问题．

一般先作出折叠前后的图形形状及位置，考虑折叠前后哪条线折叠到什么位置、哪个角折叠到哪里、哪些量相同、哪些量变化了；

然后再利用轴对称性质和相关图形性质转化相等的线段、相等的角、全等形等；

当有直角三角形出现时，考虑利用勾股定理以及方程思想来解决．

②利用轴对称变换为工具解题，主要是求最短路线问题．

一般先找出一点关于对称轴的对称点，然后连接这个对称点与另一个点的线段，与对称轴的交点即为所求的位置．

四、例题讲解

【例题2】抛物线 y＝－2/3 x^2＋7/3 x－1 与 x 轴交于点 A，B( 点 A 在点 B 的左侧)，

与 y 轴交于点 C，其顶点为 D . 将抛物线位于直线 l：y＝t ( t < 24/25 ) 上方的部分沿直线 l 向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．

(1)点 A，B，D 的坐标分别为________，________，________；

(2)如图 (1)，抛物线翻折后，点 D 落在点 E 处．当点 E 在 △ABC 内(含边界)时，求 t 的取值范围；

(3)如图 (2)，当 t＝0 时，若 Q 是“M”形新图象上一动点，是否存在以 CQ 为直径的圆与 x轴相切于点 P？若存在，求出点 P 的坐标；若不存在，请说明理由．

图(1)

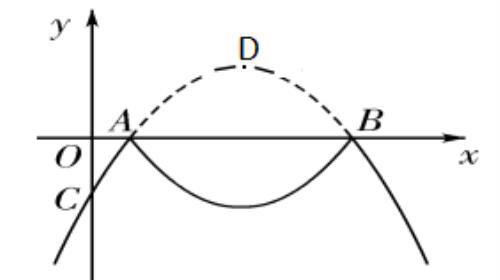
图（2）

【解题思路】

(1)利用二次函数图象上点的坐标特征可求出点 A，B 的坐标，再利用配方法即可找出抛物线的顶点 D 的坐标；

(2)由点 D 的坐标结合对称找出点 E 的坐标，

根据点 B，C 的坐标利用待定系数法可求出直线 BC 的解析式，

再利用一次函数图象上点的坐标特征即可得出关于 t 的一元一次不等式组，

解之即可得出 t 的取值范围；

(3)假设存在，

设点 P 的坐标为 ( 1/2m , 0 )，则点 Q 的横坐标为 m，

分 m＜1/2 或 m＞3 及 1/2 ≤ m ≤3 两种情况，

利用勾股定理找出关于 m 的一元二次方程，解之即可得出 m 的值，

进而可找出点 P 的坐标，此题得解．

【解答过程】

(1) 当 y＝0 时，有－2/3 x^2＋7/3 x－1＝0，

解得 x1＝1/2 ，x2＝3.

∴ 点 A 的坐标为 （1/2,0 )，点 B 的坐标为 (3,0)．

∵ y＝ －2/3 x^2＋7/3 x－1 = -2/3（x - 7/4）^2 + 25/24 ,

∴ 点 D 的坐标为 (7/4 , 25/24 ).

故答案为 (1/2 , 0)；(3,0)；(7/4 , 25/24).

(2)

∵ 点 E、点 D 关于直线 y＝t 对称，

∴ 点 E 的坐标为 (7/4 , 2t - 25/24).

当 x＝0 时，y＝－2/3 x^2＋7/3 x－1 = 0 ,

∴ 点 C 的坐标为 (0，－1)．

设线段 BC 所在直线的解析式为 y＝kx＋b，

将 B(3,0)，C(0，－1) 代入 y＝kx＋b，

∴ 线段 BC 所在直线的解析式为 y＝1/3 x－1.

∵ 点 E 在 △ABC 内(含边界)，

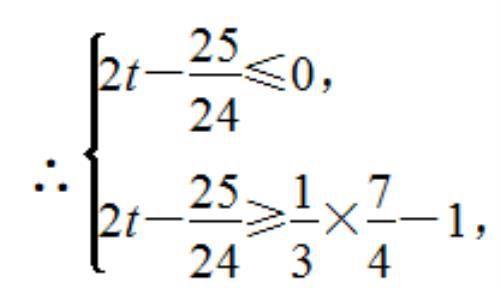
解得 5/16 ≤ t ≤ 25/48 .

(3)

当 x＜1/2 或 x＞3 时，y＝－2/3 x^2＋7/3 x－1；

当 1/2 ≤ x ≤3 时，y＝2/3 x^2－7/3 x＋1.

假设存在，设点 P 的坐标为 (1/2m , 0)，则点 Q 的横坐标为 m .

① 当m＜1/2 或 m＞3 时，点 Q 的坐标为 (m , －2/3 m^2＋7/3 m－1)(如图(3))，

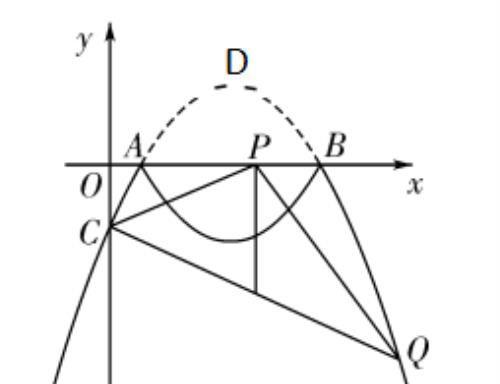
图（3）

∵ 以 CQ 为直径的圆与 x 轴相切于点 P，

∴ CP⊥PQ .

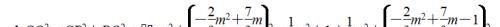
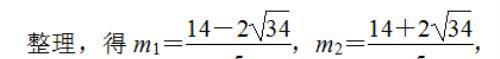
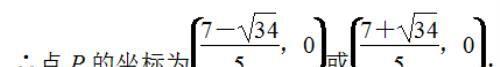
② 当 1/2 ≤ m ≤ 3 时，点 Q 的坐标为 (m , 2/3 m^2-7/3 m+1)(如图(4))，

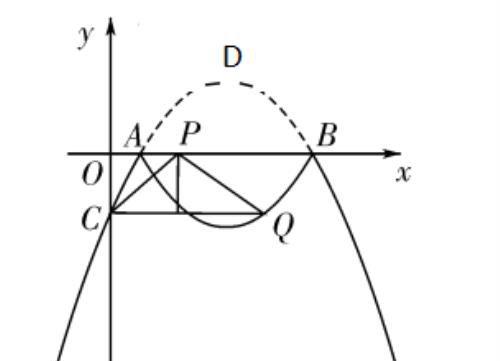
图（4）

∵ 以 CQ 为直径的圆与 x 轴相切于点 P，

∴ CP⊥PQ，

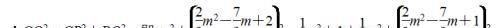
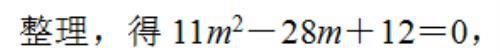
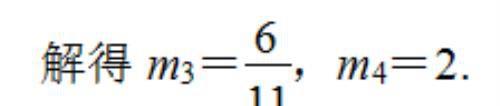
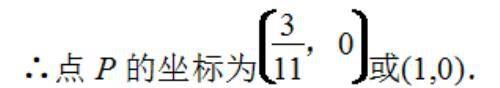
综上所述：存在以 CQ 为直径的圆与 x 轴相切于点 P，点 P 的坐标为

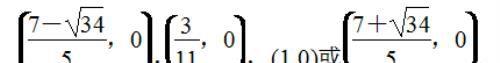
【归纳总结】

本例以翻折为背景考查了 :

一次(二次)函数图象上点的坐标特征、

待定系数法求一次函数解析式、

勾股定理以及解一元二次方程，

【解题关键】

(1)利用二次函数图象上点的坐标特征求出点 A，B 的坐标；

(2)利用一次函数图象上点的坐标特征结合点 E 在△ABC内，找出关于 t 的一元一次不等式组；

(3)分 m＜1/2 或 m＞3 及 1/2 ≤ m ≤ 3 两种情况，找出关于 m 的一元二次方程．

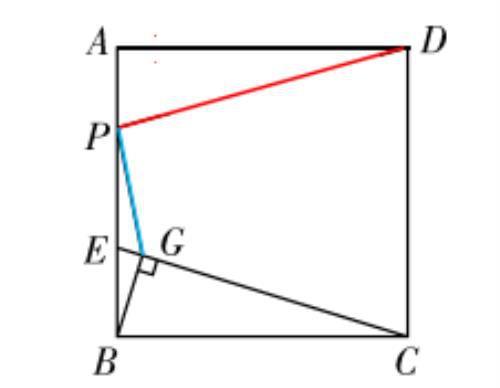
【例题3】如图，已知正方形 ABCD 的边长是 4，点 E 是 AB 边上一动点，连接 CE，过点 B作 BG⊥CE 于点 G，点 P 是 AB 边上另一动点，则 PD＋PG 的最小值为________．

【解题思路】

作 DC 关于 AB 的对称点 D′C′，以 BC 的中点 O 为圆心作半圆 O，

连 D′O 分别交 AB 及半圆 O 于 P，G .

将 PD＋PG 转化为 D′G 找到最小值．

【解答过程】

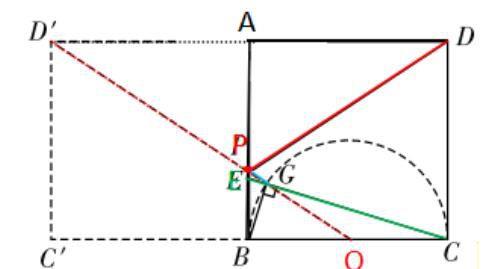
取点 D 关于直线 AB 的对称点 D′.

以 BC 中点 O 为圆心，OB 为半径画半圆．

连接 OD′ 交 AB 于点 P，交半圆 O 于点 G，连接 BG，连接 CG 并延长交 AB 于点 E.

由以上作图可知，BG⊥EC 于 G.

PD＋PG＝PD′＋PG＝D′G，

由两点之间线段最短可知，此时 PD＋PG 最小．

∵ D′C＝4，OC′＝6，

∴ D′O＝2√13 .

∴ D′G＝2√13－2 .

∴ PD＋PG 的最小值为 2√13－2.

【归纳总结】

本例题利用翻折(轴对称)确定最短最短路线问题，

通常解题思想是将线段之和转化为固定两点之间的线段和最短．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！