小学数学中的整体思想有哪些(小学数学中的整体思想教学设计)

小学数学中的整体思想

几何和图形中的整体思想

例1：一块长方形的菜地，相邻两边的长度为16米，那么长方形菜地的周长是多少米

分析：题目中要求长方形菜地的周长，我们知道长方形周长的公式为：周长=（长+宽）×2，那么我们求出长方形的长和宽就可以得到长方形的周长；但通过题目中的已知条件我们不能直接的求出长方形的长和宽各是多少，怎么办

题目中还有一个条件我们没有用，相邻两边的长度为16米，那16米就是长方形长和宽的和。

柳暗花明又一村，我们可以把（长+宽）看成一个整体，那么周长=（长+宽）×2=16×2=32（米）。

列式计算： 16×2=32（米）

答：长方形菜地的周长是32米。

例2：张爷爷利用房屋前的一面墙，用40米长的篱笆围成了一块梯形菜地（如图所示），这块菜地的面积是多少平方米

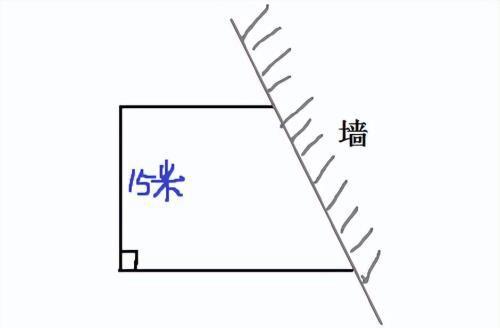
分析：通过观察图形我们可以看到这块菜地是一个直角梯形，要求它的面积，我们也知道梯形的面积公式为：S=（上底+下底）×高÷2，因为是直角梯形，那么直角边就是梯形的高，也就是15米，但是上底和下底不知道怎么办

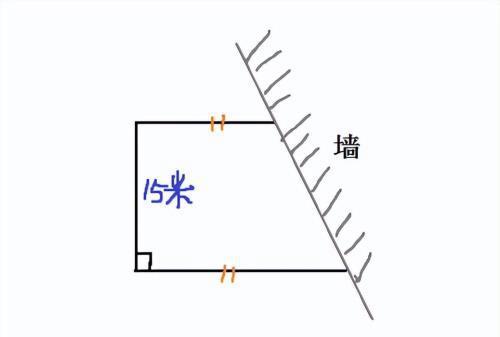
题目中还有一个条件，用了40米的篱笆，也就是说围成了一面靠墙的梯形用了40米，这40米中不包含靠墙的一面，只包含三面，三面中一面是直角边15米，另外两边也就是梯形的上底和下底，（上底+下底）=40-15=25（米），我们不用直接求出上底和下底各是多少，只需要知道上底+下底的和就可以了；所有梯形的面积S=（上底+下底）×高÷2=25×15÷2=187.5（平方米）。

列式计算：4015=25（米）……上底+下底的和

25×15÷2=187.5（平方米）

答：这块菜地的面积是187.5平方米。

例3：入图所示，正方形的面积是32平方米，求阴影部分的面积。（π取3.14）

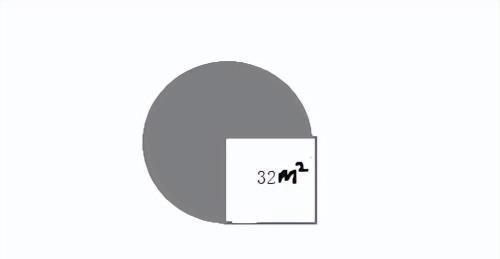
分析：通过图形我们知道正方形的面积是32平方米，也知道阴影部分是一个圆的四分之三，我们求出圆的面积，就可以得到阴影部分的面积；圆的面积公式：S=πr²，只要求出半径r等于多少就可以了；我们通过图形可以看到半径r就是正方形的边长，那么得到边长就可以，但是正方形的面积=边长×边长，32=边长×边长，边长不能直接求出来，怎么办

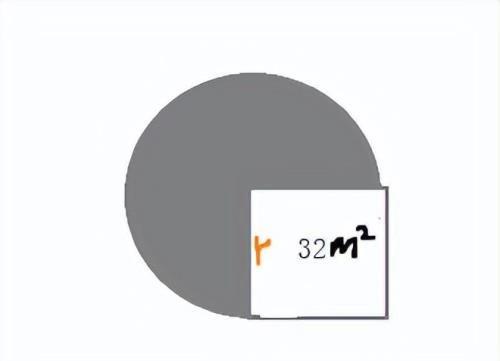
边长是半径r，圆的面积中需要r²，也就是r²=r×r=边长×边长=32，我们不用求出r，直接把r²看成一个整体，问题就迎刃而解了。先求圆的面积：S=πr²=π×32=32π（平方米）

再乘四份之三，就得到阴影部分的面积。

列式计算：32×π×=24π=24×3.14=75.36（平方米）

答：阴影部分的面积为75.36平方米。

由此看见，在小学数学几何和图形中把需要求的中间量，看做一个整体，就方便我们计算了。

免责声明:分享此文目的在于传递更多信息,,若有错误或者侵犯您的合法权益,请与我们取得联系，我们将及时进行更正、删除内容。本文内容由快快网络小婷整理编辑！