通过直线与圆交点数轻松判断直线与圆关系的方向(直线和圆的交点怎么算)

导语：通过直线与圆交点数，轻松判断直线与圆关系，相离、相交、相切

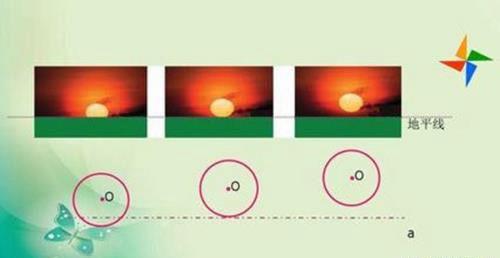
初中数学，以直线与圆交点个数来判断，直线与圆有3种位置关系。相离，直线与圆无交点；相切，直线与圆有一个交点；相交，直线与圆有两个交点。同样，我们也可以通过直线与圆心的距离来判断直线与圆的位置关系，那下面就为大家介绍一下直线与圆的位置关系。

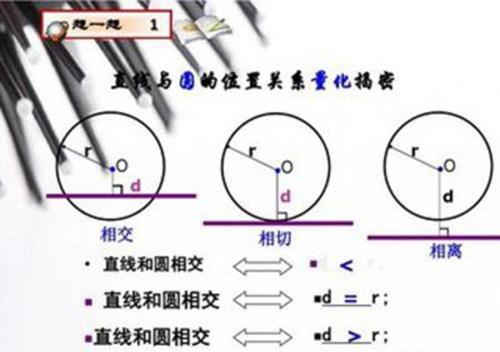
相离：就是直线与圆点的距离大于半径，与圆无交点。

相切：就是直线与圆点的距离等于半径，只有一个交点。

相交：就是直线与圆点的距离小于半径，与圆有两个交点。

直线与圆相切是直线与圆的一种特殊的位置关系，那么直线与圆相切有哪些性质特点呢。

1.直线与圆相切，那么就有直线与过切点的半径垂直。

2.从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角。

下面就列举几道相关知识点例题。

例题一：如图，四边形ABCD是⊙O的外切等腰梯形，其周长为40，则梯形ABCD的中位线长为______．

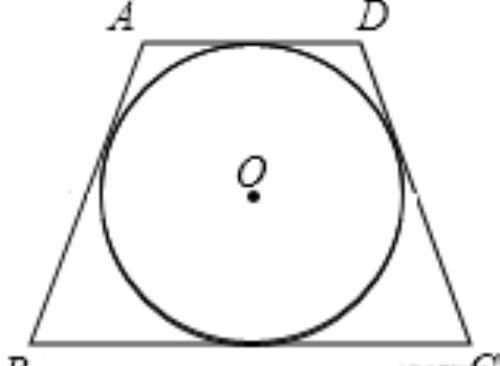
解析：设等腰梯形ABCD与圆相切点分别为E,F,G,H,如图所示

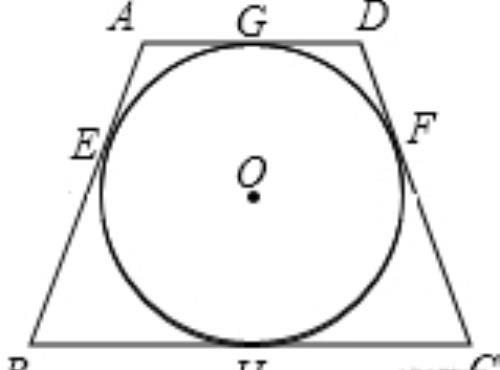
由切线长定理，我们可以得出

AE=AG,BE=BH,CH=CF,DF=DG

∴AD+BC=20

又∵梯形的中位线等于1/2（上底+下底）

∴梯形的中位线长为10

小结：本题的解题思路主要是利用里，圆外一点作圆的两条切线，那么这两条切线长相等。

例题二：已知：如图，BD为⊙O的直径，BC为弦，A为BC弧中点，AF∥BC交DB的延长线于点F，AD交BC于

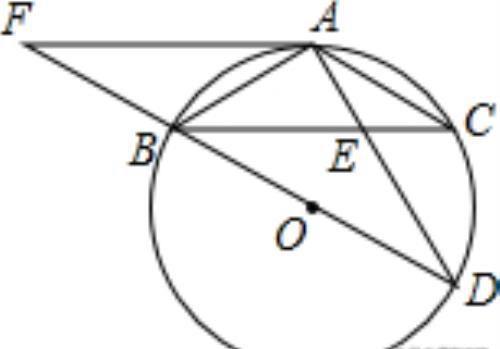
点E，AE=2，ED=4．

（1）求证：AF是⊙O的切线；

（2）求AB的长．

解析：1.连线OA，因为A为BC弧中点

∴OA⊥BC

∵AF//BC，

∴OA⊥FA FA为圆的切线。

2.∵∠BAE=∠BAD=90°

A为BC弧中点

∴ ∠ADB=∠BAC

∴△ABE∽△ABD

AB:AD=AE:AB

AB=2√3

关于直线与圆的位置关系相关的知识点，今天就为大家分享到这里，希望这些内容对大家学习有用，预祝大家学业有成。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小悦创作整理编辑！