导语：表面涂色问题——小学数学长方体和正方体的表面积问题难点突破

知识梳理

1、把一个涂色的大正方体平均分成若干个同样大的小正方体。有三个面涂色的小正方体都在大正方体顶点的位置，都是8个。有两个面涂色的小正方体都在大正方体棱的位置，个数都是12的倍数。有一个面涂色的小正方体都在大正方体的面的中心位置，个数都是6的倍数。

2、如果用n表示把大正方体的棱平均分的份数，那么

2面涂色的小正方体的个数：12（n-2）——类似正方体棱长和公式，前提是n-2

1面涂色的小正方体的个数：6（n-2）²——类似正方体表面积公式，前提是n-2

6面都不涂色的小正方体的个数：（n-2）³——类似正方体体积公式，前提是n-2

典例精析

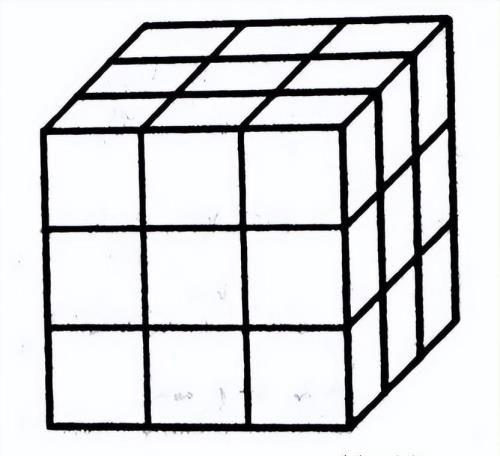
下图是由27个小正方体拼成的大正方体，把它的表面全部涂成绿色。

（1）没有涂成绿色的小正方体有几个?

（2）一面涂成绿色的小正方体有几个?

（3）两面涂成绿色的小正方体有几个?

（4）三面涂成绿色的小正方体有几个?

分析：首先确定大正方体的棱被平均分成了3份（27=3×3×3），再运用各个计算公式

解答：（1）没有涂色：（3-2）³=1（个）

（2）一面涂色：6×（3-2）²=6（个）

（3）两面涂色：12×（3-2）=12（个）

（4）三面涂色：8个

牛刀小试

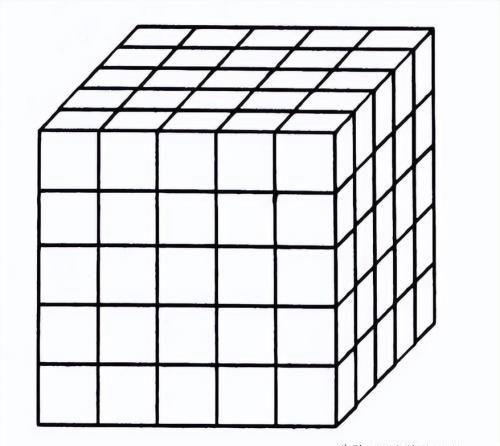
下图是由125块大小相同的小正方体拼成的大正方体模型。将其表面涂上红色。

三面涂色的有（ ）个，两面涂色的有（ ）个，一面涂色的有（ ）个，没有涂色的有( ）个。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小茹创作整理编辑！