证明角度之间的关系方法(证明角度的方法总结)

导语：一道高中题-证明角度关系

一道高中题-证明角度关系

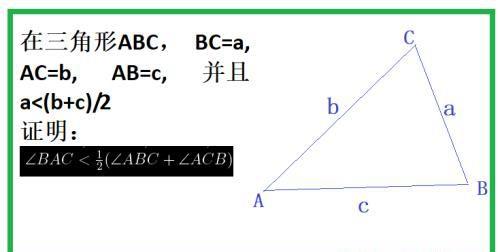
在三角形ABC， BC=a, AC=b, AB=c, 并且a<(b+c)/2

证明：

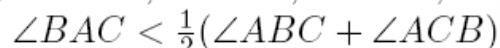
证明：证法1，

我们用A=∠BAC， B=∠ABC，C=∠ACB来代表要证明的角度，因此证明转化为：

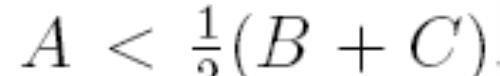
而B+C=180°-A，

则转化为要证明：

A<(180°-A)/2

即要证明A<60

根据已知：

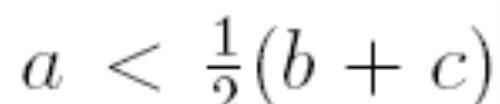
所以：

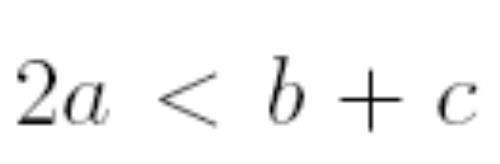
两边平方：

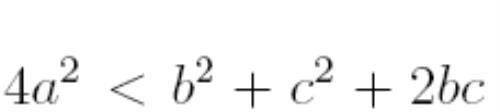
另外在三角形ABC中， 利用余弦定理：

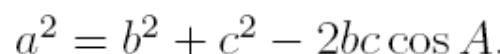
带入有：

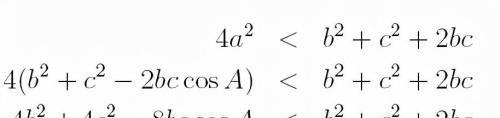
因为：

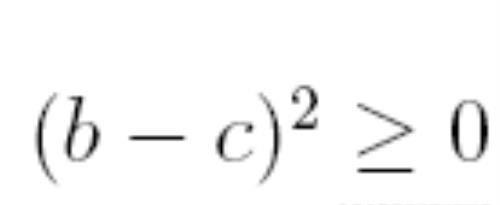
所以：

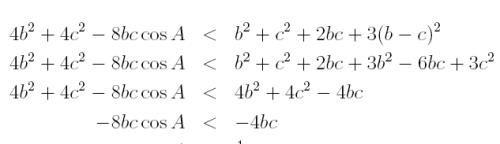
因为a是b和c 的算数均值，所以a不是最大的边长，因此A不可能是钝角。

又根据函数y=cosx 在［0，π/2］之间单调递减，所以：

A<60°

这样依次反推就证明了：

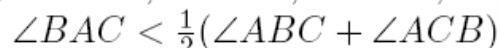
证法2： 利用正弦定理，

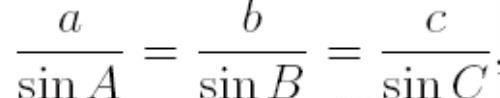
这样：

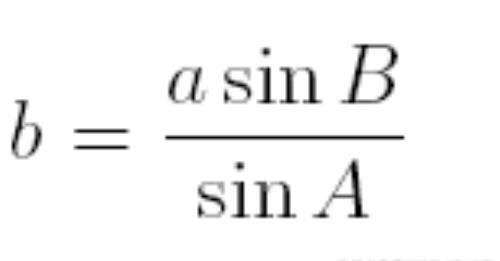
以及：

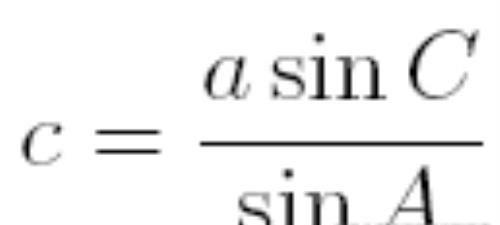
带入已知的的不等式：

有：

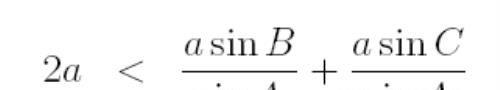
即：

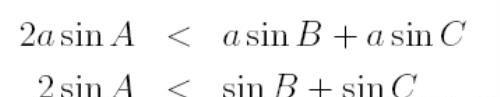
接下来利用三角的和差化积公式：

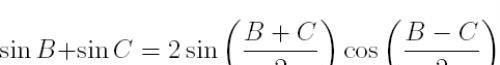
因为对于三角形中的任何角度有

Cosx小于或等于1，

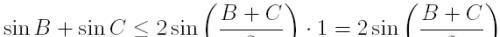
因此有：

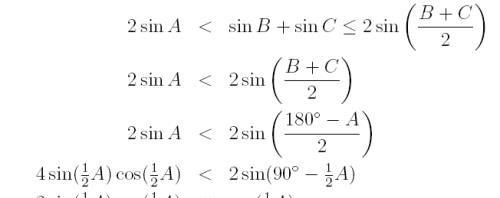
因为0°<A<180°, 所以0°<A/2<90°,

此外根据a是b和c的平均值，所以a边不是最长的，所以A是个锐角，

所以

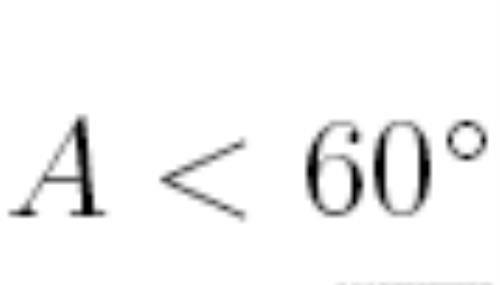
这样：180°-(B+C)<60°

60°<(B+C)/2

即A<(B+C)/2

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小奈创作整理编辑！