基本图形分析法全等三角形问题如何分析(全等三角形的基本图形基本方法思路)

导语：基本图形分析法：全等三角形问题如何分析？首先想想轴对称型

今天开始《基本图形分析法》就进入到下一个知识点章节，全等三角形的第一部分——轴对称型。

按照惯例，开始之前首先梳理出在拿到类似的几何题后，明白各种情况的分析思路。也是基本图形分析法"三步曲"式思考的第一步。

【分析方法导引】

在几何问题中，对于线段相等或角相等的问题，如果不是直接与某一基本图形的应用条件相联系时，则应先分析或观察相等的线段或角所具有的位置特征或位置关系。

如两条相等的线段或两个相等的角出现在一个等腰三角形的轴对称部分，或者也可以是出现在等腰梯形等轴对称图形的对称部分时，就可以想到要应用轴对称型全等三角形的基本图形进行分析。接下来就可以根据图形的轴对称部分找到相应的全等三角形，当完成分析的思路尚不完全清晰时，可将图形中出现的各对全等三角形全部列出，再从中筛选出与条件或结论有联系的一对或若干对全等三角形，然后再应用全等三角形的性质来完成分析。

如果几何问题中出现了两条相等的线段或两个相等的角是关于某一直线或线段成轴对称时，具体地说也就是两条相等的线段在某一直线的两侧，且在直线上同一点与直线成等角时，就可以想到要应用轴对称型全等三角形进行证明。接下来就应看图形中的对称轴有否出现，若对称轴尚未出现的，则首先考虑将对称轴添上，若对称轴已经出现的，则再看对称轴两侧的对称图形是否完整，如某一部分尚不完整的，则应将其添出，也就是应将对称轴一侧的图形，主要是三角形，沿对称轴翻折过去。然后就可以找出图形中出现的所有的全等三角形，并根据与条件、结论的联系，并应用全等三角形的性质来完成分析。

看完这些，是不依然还是迷迷糊糊的。那么直接进入正题，下面这道几何题就会用到分析方法导引中所描述的分析方法，且根据几何的基本图形性质，来一步步将分析结果展现出来，更能直观的明白几何题的思维和分析方法。

例1 如图5-1，已知：△ABC中，AB=AC，BD、CE分别是∠B、∠C的角平分线。求证：BD=CE。

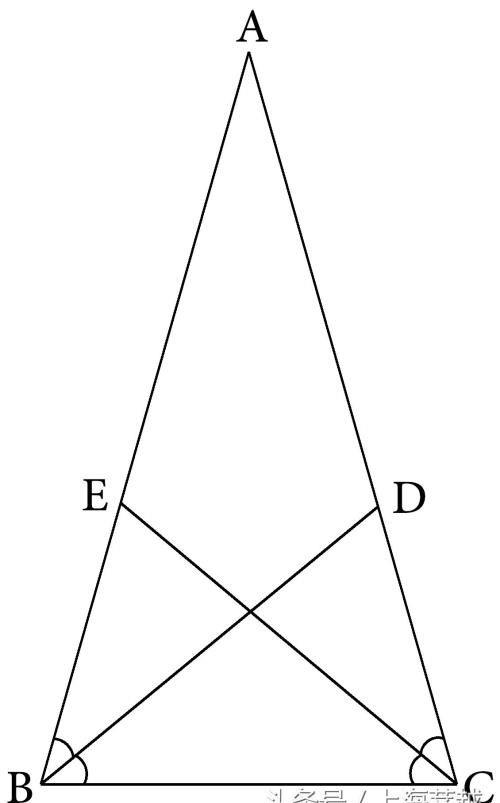
图5-1

分析：本题要证明相等的两条线段BD、CE是等腰三角形的两底角平分线，它们位于这个等腰三角形的轴对称部分，所以可应用轴对称型全等三角形进行证明。

根据由图形的轴对称部分找全等三角形的方法，可以发现图形中出现的轴对称型全等三角形共有三对，而以要证明相等的线段BD、CE为边的全等三角形则是其中的两对，所以选用哪一对全等三角形进行证明就出现了两种可能性。分别是（1）△ABD和△ACE；（2）△BDC和△CEB。

（1）若将BD、CE看作是△ABD和△ACE的一组对应边，那么在△ABD和△ACE中，已经给出了AB=AC，∠A=∠A是公共角，所以还要证明一个性质。由条件△ABC是等腰三角形，应用等腰三角形的性质可得∠ABC=∠ACB，而BD、CE是角平分线，所以∠ABD=∠ACE，从而就可以证明这两个三角形全等。

（2）若将BD、CE看作是△BDC和△CEB的一组对应边，那么在△BDC和△CEB中，由AB=AC，可得∠BCD=∠CBE，BC=CB是公共边，再由BD、CE是角平分线，又可得∠CBD=∠BCE，所以这两个三角形全等也可以证明。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！