什么是正定二次型矩阵(正定二次型如何判断)

导语：线性代数之正定二次型和正定矩阵的判定方法总结

正定二次型和正定矩阵的知识点：

正定二次型的定义：

正定二次型的定义

正定二次型的判定方法：

正定二次型的判定方法

题型一：正定型的判别

例1：

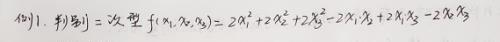
解法一：写出二次型对应矩阵A，并用A的全部顺序主子式大于0判别。

利用顺序主子式大于0进行判别

解法二：二次型为正定二次型当且仅当A的全部特征值大于零。

利用矩阵的特征值大于零进行判别

题型二：已知二次型为正定二次型，求参数的取值范围。

例2：

解题思路：二次型为正定二次型当且仅当矩阵A对应的顺序主子式全大于零。

解：

题型三：正定二次型的证明

例3：已知n阶矩阵A是正定矩阵，证明A的伴随矩阵也是正定矩阵。

证明：

总结：n阶矩阵A正定时，与A有关的如下矩阵也是正定矩阵：

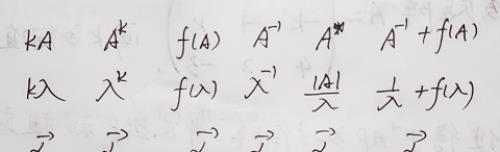
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小嫣创作整理编辑！