无穷不尽什么意思(有没有无穷无尽这个词)

导语：这里有无穷无尽的不等式，只要你的脑洞足够大

你有没有想过，凸函数的定义不等式，竟然可以派生出无穷无尽的不等式。只要你的脑洞足够大，所有不等式都可以从中派生出来，当然也包括那些世界闻名的不等式。甚至有可能派生出新的重要不等式来。

凸函数的定义不等式的定义不等式有两个形式。一个是上凸函数的定义不等式，一个是下凸函数的定义不等式。它们的不等号方向正好是相反的。

上凸函数比如自然对数函数y=lnx，a小于0的二次函数y=-x^2等。上凸函数的定义不等式描述的是，曲线上任意两点间的任意点，都在经过这两点的割线上竖直对应点的上方。用不等式表示为：f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2)。

下凸函数比如e的指数函数y=e^x，a大于0的二次函数y=x^2等。下凸函数的定义不等式描述的是，曲线上任意两点间的任意点，都在经过这两点的割线上竖直对应点的下方。用不等式表示为：f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2)。

x1, x2就是曲线上的任意两点的横坐标。λ是小于1的正数。

那你有没有想过，任意凸函数都会有它自己的定义不等式。比如：对任意实数a,b, 有e^((a+b)/2)≤(e^a+e^b).

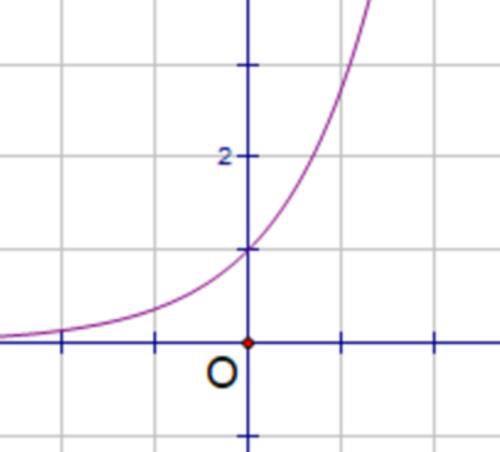
它其实是对下凸函数y=e^x的定义不等式的一个直接运用。a, b是曲线上任意两点的横坐标，这里取λ=1/2. 对它的证明自然是轻而易举的了。由于y=e^x是严格上凸的，所以这里当且仅当a=b时，才取不等式的等量关系。

而当a,b取不同的值时，就会产生无穷无尽的不等量关系。

比如：根号e<(1+e)/2, e^2<(e+e^3)，e^0.2<(e^0.1+e^0.3)/2, e^(-1)=(e+e^(-3)),……

相信只要你稍一动脑筋，就会发现，上面这一系列的不等式，只是均值不等式的一些特例。不过并非所有的凸函数派生出来的不等式，都是均值不等式的特例。比如：对任意非负实数a,b, 有2arctan((a+b)/2)≥arctana+arctanb.

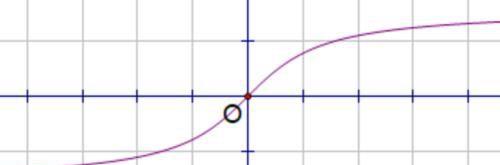
反正切函数y=arctanx与y=e^x在凸性上有很大的不同，y=e^x在R上是严格下凸的，而y=arctanx则在非负区间严格上凸，在非正区间严格下凸。在这方面，y=arctanx由定义不等式，可以直接派生出两个不等式。包括对任意非正实数a,b, 有2arctan((a+b)/2)≤arctana+arctanb.

同样当仅且当a=b时，才取它们的等量关系。也同样的，当a,b取不同的值时，也会派生出更多不一样的不等式，比如：arctan(a+b)≥(arctan(2a)+arctan(2b))/2, (a,b非负).

甚至，如果凸函数的定义公式派生出来的不等式，与其它不等式结合起来，就有可能派生出更多不一样的不等式来了。比如，上面提到的不等式e^((a+b)/2)≤(e^a+e^b)，如果结合不等式e^x≥1+x，就可以派生出不等式：1+(a+b)/2≤(e^a+e^ b)/2.

加上各个凸函数派生出来的不等式之间也可以互相结合。因此，老黄有理由相信，所有的不等式，都可以在这个体制下派生出来。只是老黄的脑洞还不够大。目前还没有更重要的发现而已。老黄不行，不代表你不行哦。大家一起来努力，说不定会有意外的惊喜哦。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小舻创作整理编辑！