求函数值的五种常用方法(求函数值的三种基本方法)
求函数最值的问题,相信大家都不陌生。平时我们用得最多的方法,比如运用二次函数的顶点式求最值,利用均值不等式求最值,以及利用函数的单调性求最值的方法等。这些都不是老黄所说的一般方法,它们是常用的方法,并不能适用一般函数。
那到底什么样的方法才适用求一般函数的最值呢?这种方法是通过比较函数最值可能出现的各类点的函数值的大小来确定最值的。在局部,极值就是最值。因此,最值可能出现在极值点上。极值点有两类,一类是函数的稳定点,即使f'(x)=0的点,另一类是不可导点。加上区间端点,所有这些点上的函数值,就肯定包含了函数的最值。
因此,求函数最值的一般方法就是:比较函数所有稳定点、不可导点和区间端点上的函数值.
下面通过解决一道例题,来学会运用一般方法求函数最值的具体操作。
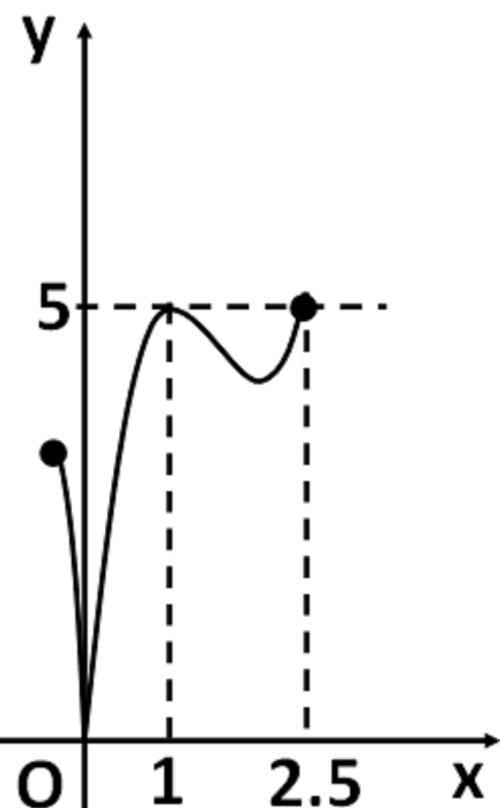
例:求f(x)=|2x^3-9x^2+12x|在闭区间[-1/4,5/2]上的最值.
解:当f(x)=|2x^3-9x^2+12x|=0时,x=0,【这里x=0就是函数的不可导点,f(0)=0就有可能是函数的最值】
∴f’(x)=|6x^2-18x+12|, (x≠0).【对于可导的区间,对函数求导,目的是确定函数的稳定点】
当f’(x) =|6x^2-18x+12|=0时,x=1或x=2. 【得到函数的两个稳定点,下面就可以开始求各点的函数值了,老黄采用自变量从小到大的顺序,总之不要漏掉就可以了】
f(-1/4)=|2×(-1/4)^3-9×(-1/4)^2+12×(-1/4)|=3又32分之9.
f(1)=|2-9+12|=5,
f(2)=|2×2^3-9×2^2+12×2|=4,
f(5/2)=|2×(5/2)^3-9×(5/2)^2+12×(5/2)|=5.
∵0<3又32分之9<4<5,所以f(0)=0最小,f(1)=f(5/2)=5最大.
函数的图像大致如图:
总结求函数最值的一般步骤如下:
1考虑使用常用的方法;不是说有一般方法,我们就可以不要常用的方法了。如果用常用方法可以解决的问题,我们当然还是要优先使用常用方法的。
2找出函数的不可导点;
3求稳定点(使f’(x)=0的点);至于这个点是不是极值点,是极大值点还是极小值点,在这里并不重要。最后比较函数大小就可以了。
4求各点的函数值(包括端点);如果是开区间的端点,就求极限,假如这个极限最大或最小,那么函数就没有对应最值。
5比较各函数值,确定最值。
现在您会求一般函数的最值了吧!
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小纳创作整理编辑!