数学准备

统计量：用于描述数据特征，比如描述集中趋势和离散程度

集中趋势

均值（平均数，平均值）（mean）

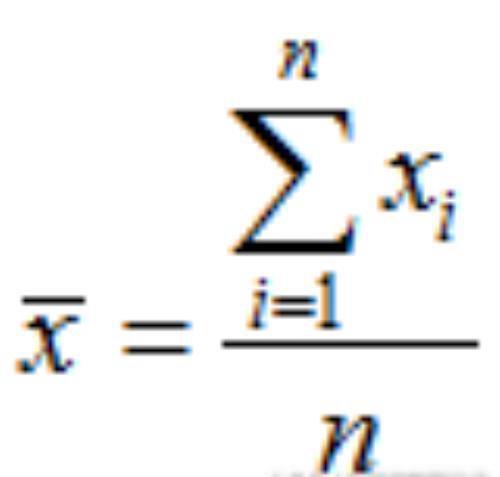
中位数 （median）: 将数据中的各个数值按照大小顺序排列，居于中间位置的变量

给数据排序：1， 2， 2， 6， 9，找出位置处于中间的变量：2，2就是中位数

当n为基数的时候：直接取位置处于中间的变量 当n为偶数的时候，取中间两个量的平均值

众数 （mode）：数据中出现次数最多的数

离散程度

方差

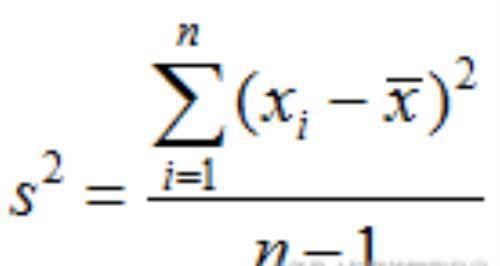
标准差

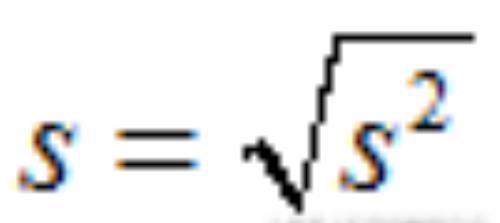
简单线性回归介绍

简单线性回归包含一个自变量(x)和一个因变量(y)，以上两个变量的关系用一条直线来模拟。如果包含两个以上的自变量，则称作多元线性回归分析(multiple regression)

简单线性回归模型

被用来描述因变量(y)和自变量(X)以及偏差(error)之间关系的方程叫做回归模型

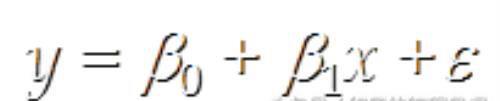
关于偏差ε的假定

ε是一个随机的变量，均值为0

ε的方差(variance)对于所有的自变量x是一样的

ε的值是独立的

ε满足正态分布

简单线性回归方程

E(y) = β0+β1x

这个方程对应的图像是一条直线，称作回归线

其中，β0是回归线的截距，β1是回归线的斜率 ，E(y)是在一个给定x值下y的期望值（均值）

x和y是有一下三种关系的

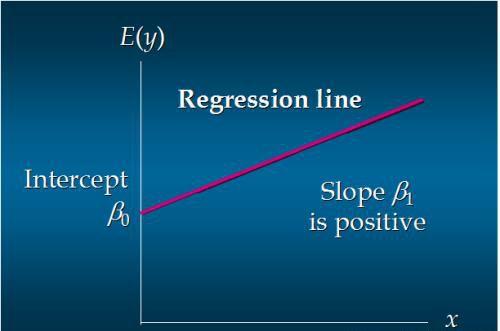
正线性关系

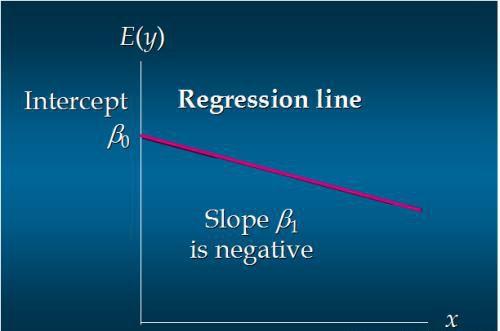
负线性关系

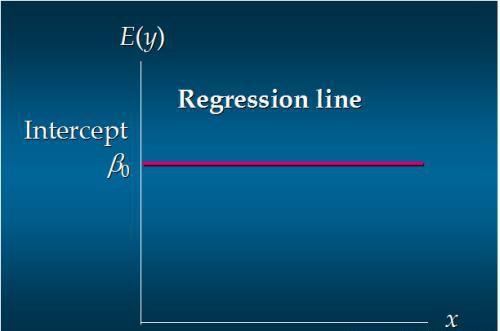
无关系

估计的简单线性回归方程

ŷ=b0+b1x，这个方程叫做估计线性方程(estimated regression line)

其中，b0是估计线性方程的纵截距，b1是估计线性方程的斜率，ŷ是在自变量x等于一个给定值的时候，y的估计值

线性回归分析流程：

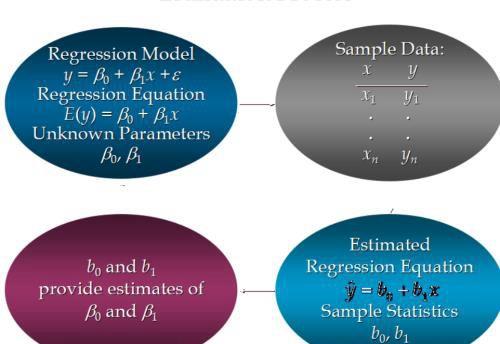
首先存在一个真实的模型，它的关系是

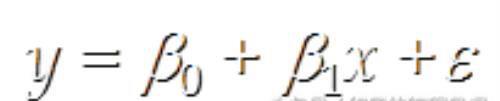
我们由它得到回归方程

E(y) = β0+β1x

然后通过具体数据集来估计出β0和β1也就是b0和b1

β0和β1是真实的关系，数据集x和y肯定是存在这样的一种关系，而这种关系太难以掌握我们可以估计出它们，也就是相近的值b0和b1

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小姿创作整理编辑！