中考越来越近，留给考生的复习时间也越来越少，在这个节骨眼上，很多考生都会把时间用在专题复习上面。确实，如果在中考来临之前，能尽快吃透一些常考的热点专题，这将会帮助考生提高数学成绩，提升中考信心。

在现代数学教育理念引导之下，中考作为选拔人才的考试，其地位也越来越重要。近几年来的中考数学试题，除了对基础知识进行全面考查之外，同时会特别突出了对考生综合能力的考查，因此，在全国各地很多中考数学试卷中，出现了大量内容丰富、形式多样的能力型试题。

​如一些综合问题会以二次函数为载体，探究由二次函数上的点能否构造成特殊的四边形的存在性压轴题。此类问题主要依据特殊四边形的性质定理为基础，同时蕴含着丰富的数学思想方法，像待定系数法、数形结合、分类讨论等思想方法是解决此类问题的关键。

解决这类问题的关键：一定要弄清函数与几何图形之间的内在联系，在解题过程中将函数问题几何化，几何问题数量化，体现数形结合的思想。

​二次函数与四边形的存在性问题，讲解分析1：

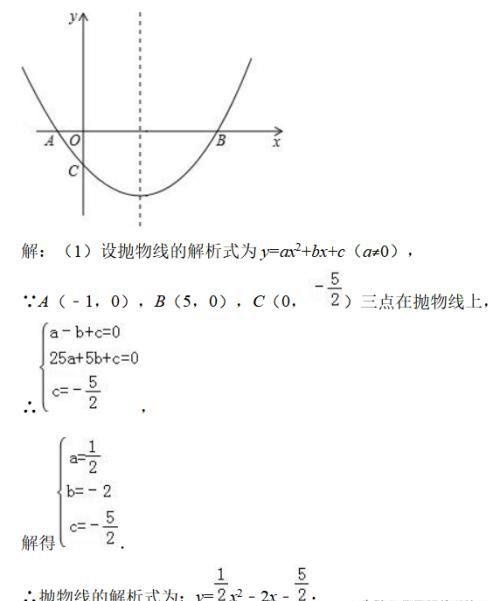
如图，抛物线经过A（﹣1，0），B（5，0），C（0，-5/2）三点．

（1）求抛物线的解析式；

（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

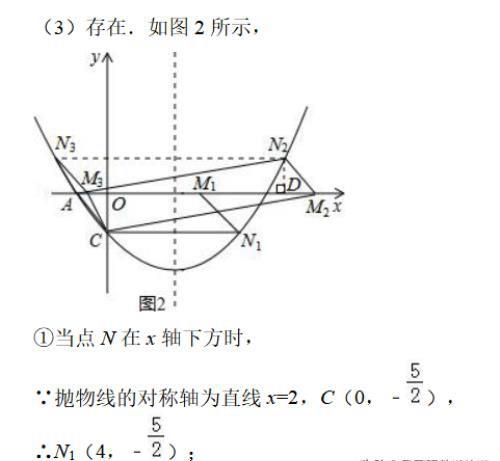
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

​

​

​

​题干分析：

（1）设抛物线的解析式为y=ax2+bx+c（a≠0），再把A（﹣1，0），B（5，0），C（0，-5/2）三点代入求出a、b、c的值即可；

（2）因为点A关于对称轴对称的点B的坐标为（5，0），连接BC交对称轴直线于点P，求出P点坐标即可；

（3）分点N在x轴下方或上方两种情况进行讨论．

解题反思：

本题考查的是二次函数综合题，涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识，在解答（3）时要注意进行分类讨论。

​以二次函数为载体、满足某种条件的几何图形是否存在的问题，一直是中考数学的热点和难点。

由二次函数上的点构成平行四边形的存在性问题由二次函数上的点构造平行四边形的压轴题，往往是给了平行四边形上的两个顶点，另外两个顶点中有一个在二次函数上，求二次函数上的这个顶点的坐标等。

二次函数与四边形的存在性问题，讲解分析2：

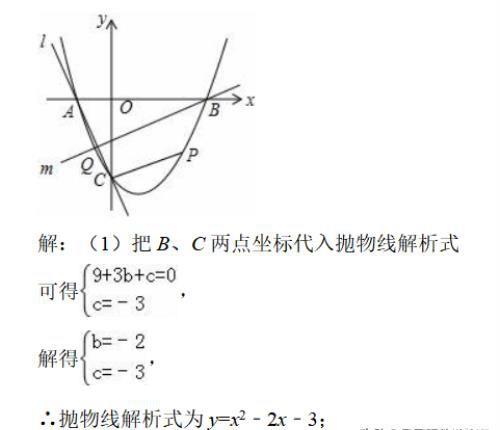
如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）

（1）求抛物线的解析式；

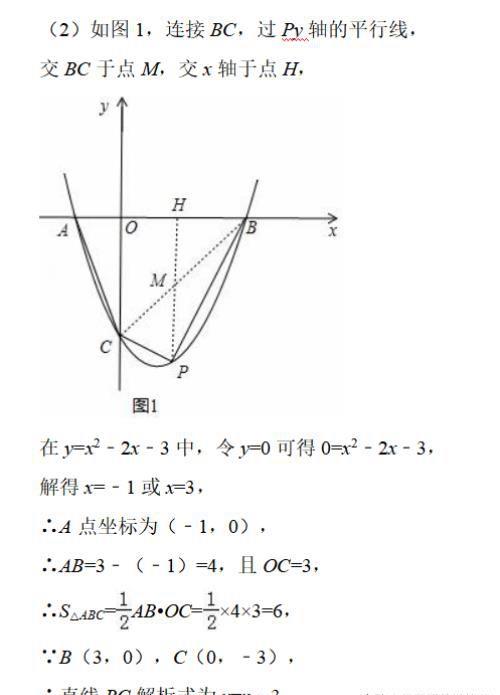
（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P的坐标和四边形ABPC的最大面积．

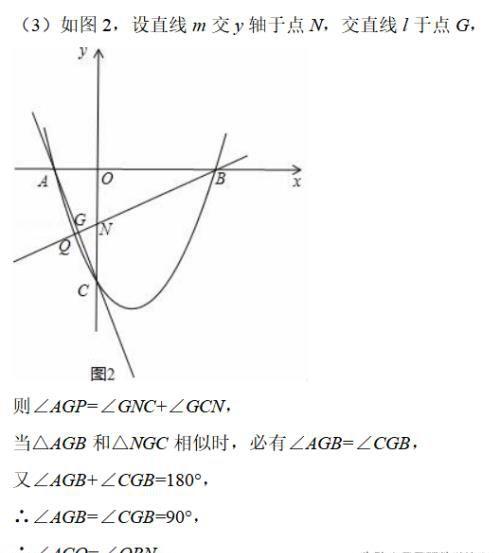
（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．

​

​

​

​

​

考点分析：

二次函数综合题．

题干分析：

（1）由B、C两点的坐标，利用待定系数法可求得抛物线的解析式；

（2）连接BC，则△ABC的面积是不变的，过P作PM∥y轴，交BC于点M，设出P点坐标，可表示出PM的长，可知当PM取最大值时△PBC的面积最大，利用二次函数的性质可求得P点的坐标及四边形ABPC的最大面积；

（3）设直线m与y轴交于点N，交直线l于点G，由于∠AGP=∠GNC+∠GCN，所以当△AGB和△NGC相似时，必有∠AGB=∠CGB=90°，则可证得△AOC≌△NOB，可求得ON的长，可求出N点坐标，利用B、N两的点坐标可求得直线m的解析式．

解题反思：

本题为二次函数的综合应用，涉及知识点有待定系数法、二次函数的最值、相似三角形的判定、全等三角形的判定和性质等．在（2）中确定出PM的值最时四边形ABPC的面积最大是解题的关键，在（3）中确定出满足条件的直线m的位置是解题的关键．本题考查知识点较多，综合性较强，特别是第（2）问和第（3）问难度较大。

​

​二次函数与四边形的存在性问题，讲解分析3：

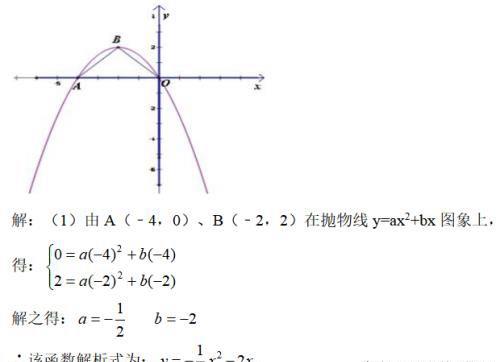
如图，抛物线y=ax2+bx经过点A（﹣4，0）、B（﹣2，2），连接OB、AB，

（1）求该抛物线的解析式．

（2）求证：△OAB是等腰直角三角形．

（3）将△OAB绕点O按逆时针方向旋转135°，得到△OA′B′，写出A′B′的中点P的坐标，试判断点P是否在此抛物线上．

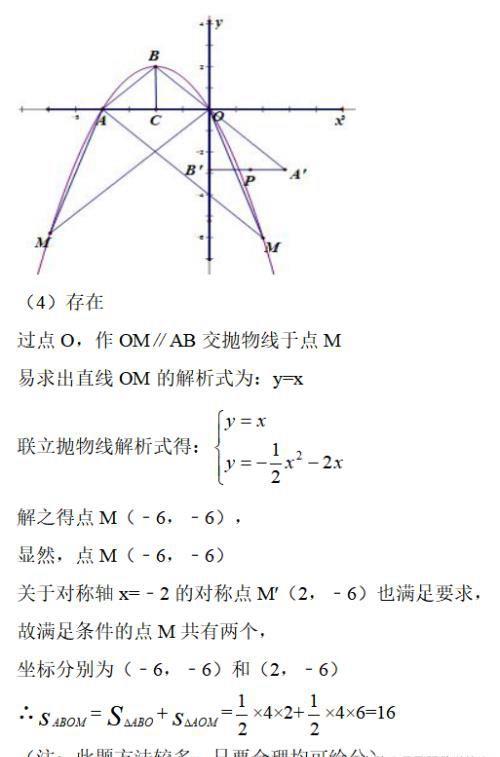
（4）在抛物线上是否存在这样的点M，使得四边形ABOM成直角梯形，若存在，请求出点M坐标及该直角梯形的面积，若不存在，请说明理由．

​

​

​考点分析：

二次函数综合题；综合题。

题干分析：

（1）将A（﹣4，0）、B（﹣2，2）代入抛物线解析式y=ax2+bx，列方程组求a、b的值即可；

（2）根据所求抛物线解析式求抛物线的顶点坐标，判断三角形的形状；

（3）根据△OAB的形状，旋转方向，旋转角，画出图形，可求A′、B′的坐标，根据中点坐标公式求P的坐标，代入抛物线解析式进行判断；

（4）存在．过点O，作OM∥AB交抛物线于点M，根据△OAB为等腰直角三角形，可求直线OM的解析式，与抛物线解析式联立，可求M点坐标，同理，过点A，作AM′∥OB交抛物线于点M′，联立方程组可求M′的坐标，由图形的特殊性可知，两种情况下，梯形面积相等，根据梯形面积公式求解．

解题反思：

本题考查了二次函数的综合运用．关键是根据题意求抛物线解析式，根据解析式确定图形的特殊性。

从近几年的试题分布情况来看，解决二次函数与四边形有关的存在性问题，它的一般解题步骤可以归纳如下：

一是假设其存在，画出相应的图形;然后根据所画图形进行解答，得某些结论；二是如果结论符合题目要求或是定义定理，则假设成立；三是如果出现与题目要求或定义定理相悖的情况，则假设错误，所设不存在。

以二次函数相关知识定理为命题背景，探究由二次函数上的点构造特殊四边形的压轴题，一直是中考数学的重难点，考生在复习阶段，一定要加以重视。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小若创作整理编辑！