图的邻接矩阵和邻接表存储(图的邻接矩阵存储结构定义)
图的基本概念
概念引入
可以简单的说，图是由一些点，和连接点的线组成。
点就是图的结点（顶点）。
线就是路径（边）。
（图1-1 简单的图）
关于边
边权：表示两个结点之间连线的距离（如结点3 到 结点2 的距离是 6 ）
（图1-2 有权图）
（图1-3 无权图）
跟道路一样，边有的时候只允许从A到B，不允许从B到A。
无向边：没有箭头的线，可以互相到达
有向边：有箭头，只能从箭头末端到箭头指向，如（1-4中 只能从 结点1 到 结点2 ）
（俩个结点间可以有俩条有向边，表示它们是互通的，此时跟无向边等效）
根据有无 有向边，图分为有向图与无向图。
有向图：只要存在有向边就是有向图。
无向图：不存在有向边。
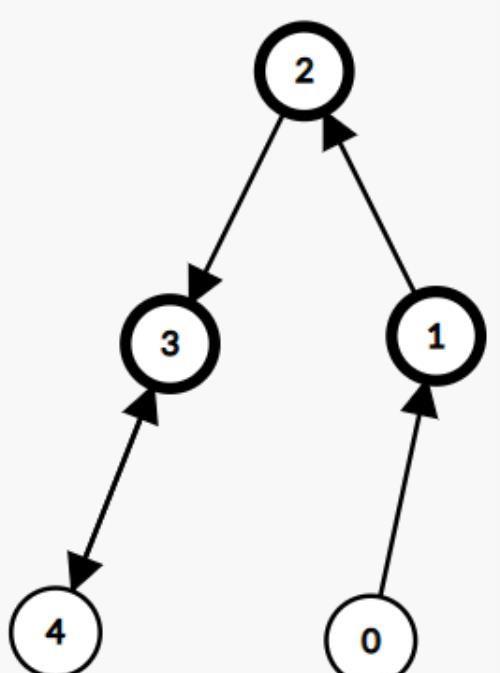
（图1-4有向图）
图1-5
关于点
度：在无向图中，在一个点所连接的边的个数 称为度。入度：在有向图中，进入该点的边的个数出度：从该点出去的边的个数。图1-5 中 3的度数为2
图 1-4 中 3的入度为2，出度为0
总结
图的元素有：
顶点（Vertex） 边（Edge）和 边权（Weight）
边分为有向边与无向边
扩展概念
边权全为1 的图叫做无权图，否则叫有权图。（如未说明权重，可视为无权图）
（图1-2 有权图）
（图1-3 无权图）
路径：一系列由边相连的点，如1-7 中的 2，1，5，0是一条路径；4，3，2是一条路径。
（图 1-7）
简单路径：不重复经过一个点两次的路径，如1-7中 2，1，5，0是一条简单路径，但2，1，5，0，1不是一条简单路径，因为1经过了两次。回路：回路是一种路径，起点和终点相同的路径。如 1，5，0，1是一个回路，2，1，5，0，1，2也是一个回路。简单回路：是只有起点和终点能重复两次的路径。如 1，5，0，1是一个简单回路，但2，1，5，0，1，2不是一个简单回路。因为除了起点2以外，1也被经过了两次。环：不做特殊说明时，就是简单回路。连通图：在无向图中，每两个点都可以相互到达。子图：取原图中一部分的点和边构成的图
图的简单概述
完全图：
无向图：若每对顶点之间都有一条边相连，则称该图为完全图
有向图：若每对顶点之间都有两条有向边相连，则称该图为完全图
无向图
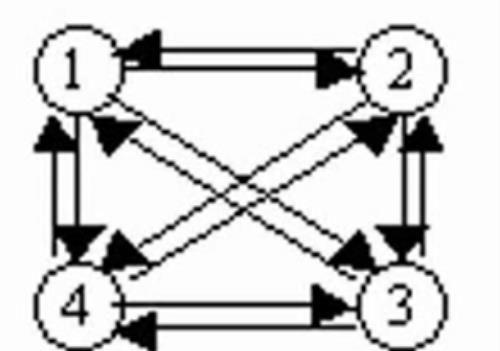
有向图
图的存储
存图的常见方法有两种：
1. 邻接矩阵
2. 邻接表
邻接矩阵
用一个n阶的方阵来存放图中各结点的关联信息。（如使用二维数组）
int g][]; 若 R[ i ][ j ]
等于 1 ，表示结点 i 到结点 j 有一条邻接边（有向边）等于 0 ，表示结点 i 到结点 j 没有邻接边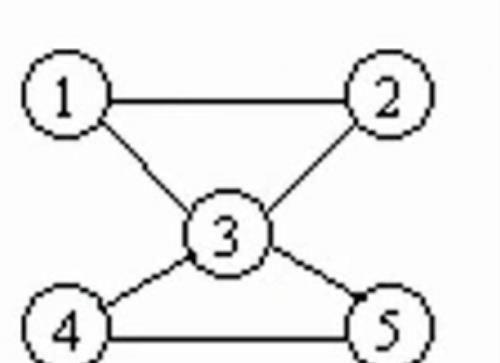
该图下标从1开始
如上图中，因为 1 到 2 和 2 到 1 有一条邻接边，所以有R[1][2] = R[2][1] = 1;
通过这样记录图可以得到上面的二维数组。
通过上面我们可以看出，无向图的邻接矩阵关于斜边对称。所以可以通过用上三角或下三角矩阵存无向图来节省空间。邻接表
用链表来实现
首先把每个结点的邻接结点用一个链表表示出来，这时我们可以得到n个链表 （n为结点数）然后用一个一维数组来顺序存储每个链表的头指针（即对应的结点）
对于V1 结点，它的邻接结点有 V2、V4、V6，分别距离为6、1、50。所以在V1的链表中，我们如下这样记录[2][6]--[4][1]--[6][50]（表示到达V2距离6，到达V4距离1，到达V6距离50）。最后把所有链表放在一个一维数组中，得到如下的邻接表。
应用情况
（邻接矩阵只适用于没有重边（或重边可以忽略）的情况，一般情况下不用考虑）
邻接矩阵空间复杂度高：为O(n^2)查询一条边的存在情况快： O(1)遍历一个点的所有出边 ：O(n)遍历整个图 ：O(n^2)邻接表邻接表基本可以应对所有情况（除了要快速查询一条边要用邻接矩阵）
空间复杂度低 ：为O(m) m为边数查询某条边 ： O(d+(u))即这个点的边数 ，如果边有排序，则通过二分就是O(log d+(u)) log边数的事件。遍历一个点的所有出边 ：O(d+(u))即该点的边数遍历整个图 ：O(n+m) 事件为点的个数加边数。总结：快速查询时用邻接矩阵，其余情况用邻接表。
如果觉得有帮助的话，可以收藏，点赞支持一下哦！
免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小碧创作整理编辑！