数学中的烙饼问题(烙饼问题中的数学思想)

在教学中，怎么做能让学生由感性经验到数学模型，怎样理解“烙饼问题中的最短时间”？可以这样安排活动：

活动过程

1.明确题意，理解“满锅”。

一个锅，每次只能烙两张饼。每个饼两面都要烙，每面3分钟。客人、妈妈和我每人1个。怎样才能尽快吃上饼？

（1）请同学默读,同桌相互说一说，已知条件是什么，问题是什么。

（2）烙1个饼需要多长时间？用实物示意图反馈烙饼过程，再用图示记录烙饼过程，椭圆表示锅，小圆表示饼，列出表格。

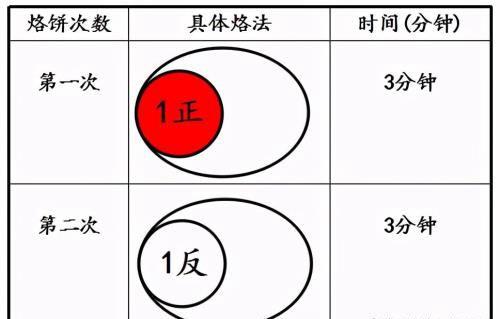
（3）烙2个饼需要多长时间？

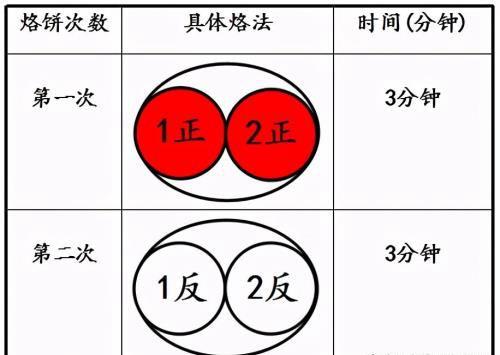
（4）比较并思考：烙1个饼和2个饼，数量不一样，为什么需要的时间却相同？烙1个饼时，锅里还有一半空着没用起来，浪费了空间；烙2个饼时，把锅充分用起来，没有浪费能量，可以叫“满锅”烙。“满锅”烙是省时的关键手段。

2.自主探索，体验“轮换”是优化的方法。

烙3个饼，怎样才能尽快吃上饼？

（1）独立思考，动手操作，用自己喜欢的方式表示烙饼过程。

（2）自主探索后，同桌说说烙饼的方法，指名边烙边说过程。

方法一：12分钟，12分钟是最少时间吗？不是，后面两次只烙1个饼，锅空着一半空间。③号饼的正面和反面不能同时烙，那怎么才能实现“满锅”呢？

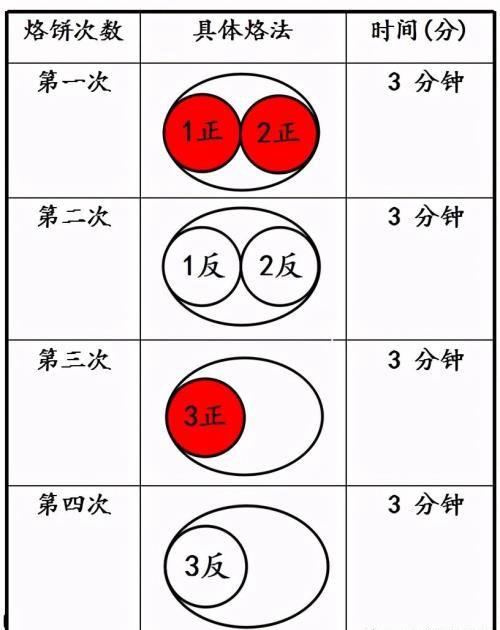
为学生营造实践感悟的空间，12分钟虽然不是最优化的结果，确是优化的思维起点和关键，有了这样的操作，学生才能从“做”到“思”，实践中体验比较中寻求，达到直观到抽象由“做”到“思”的思维升华。

方法二：3个饼一共6个面，每次烙2个面，至少烙3次。第一次是烙①号②号饼的正面，第3次烙②号③号饼的反面，那么第二次呢？①号饼的反面和③号饼的正面。烙三次的关键是什么？关键是第二次把②号饼拿出来换成3号饼。教师介绍，这种方法叫做“轮换”烙，这样可以做到3个饼“满锅”烙。

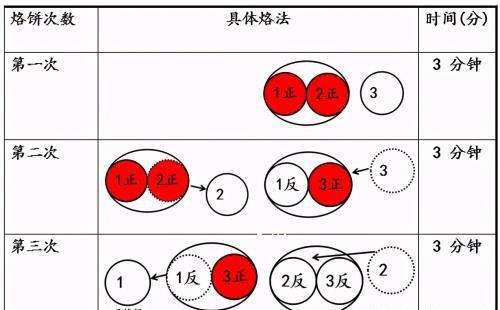
这样的学习过程，学生通过动手操作、语言表达、对比思考充分体验轮换烙饼，理解“烙饼问题中的最短时间”。

如何让动手操作真正成为数学活动经验？是按照老师的要求机械的做？还是放手让学生热闹的“做”，我认为都有偏颇，数学的操作是为了提升思维，因此动手操作不是直接做对，而是有一个经历的过程，操作“失败”才是操作的精华所在，因为“失败”带给孩子的思考最有价值。因此本课不急于用最优方法烙，而是让学生按照自己的理性经验烙，烙后在思考才发现了最优方法，将行为的感知升华为理性的思维认知，使学生发展思维能力的同时理解抽象的数学思想。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小洁创作整理编辑！