> 美食
空间向量求夹角的方法(利用空间向量求空间角公式)
利用空间向量求空间夹角问题是历年高考的热门考点,主要有三种:直线与直线、直线与平面、平面与平面的夹角。无论是哪种情形,最后都需要转化为求直线与直线的夹角问题。
(1)直线与直线所成的角:设异面直线l1,l2的方向向量分别为n1,n2,则l1与l2所成角θ满足cos θ=|cos〈n1,n2〉|;
(2)直线与平面所成的角:设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α所成角θ满足sin θ=|cos〈m,n〉|;
(3)平面与平面所成的角:
a.如图,AB、CD是二面角α-l-β的两个面内与棱l垂直的直线,它们的向量分别为m,n,则二面角的大小θ满足cosθ=cos〈m,n〉;
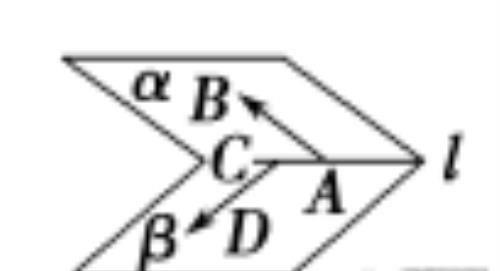
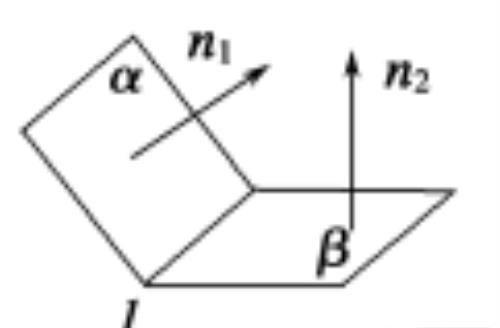
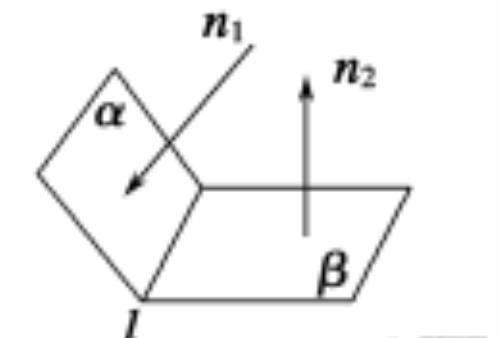
b.如图,n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cos θ=cos〈n1,n2〉或-cos 〈n1,n2〉。


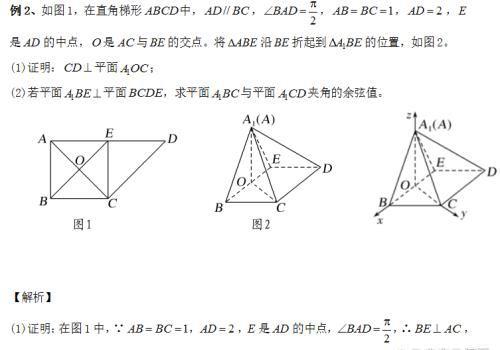

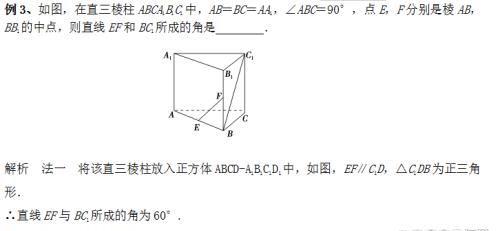

好了,今天的内容就分享到这里,如果您有疑问,可以在文章下方留言,欢迎继续关注,精彩还将继续!
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小凡创作整理编辑!