如上一篇文章所述，样本所属总体服从正态分布是数据分析和数据挖掘等数据处理的重要前提。如果我们采集的样本并不能确认其总体是否服从正态分布，那么数据处理的结果就是不可靠的。因此，对样本数据进行正态分布检验十分必要。常用的正态分布检验方法有以下几种：

1.基于偏度和峰度的假设检验

基于偏度-峰度的检验是利用了正态分布偏度(3阶矩)和峰度（4阶矩）都为0的特点。

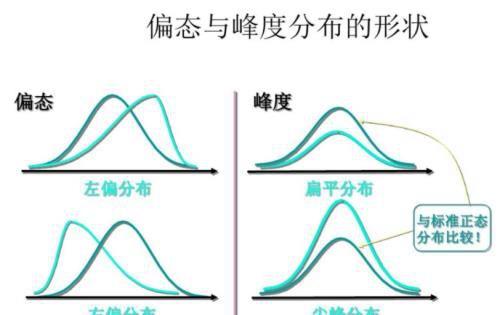
如果样本数据能满足偏度和峰度均为0的假设，则可以认为总体服从正态分布。由于该检验是基于偏度检验和峰度检验的，样本数量需要8个以上。以下normaltest函数就使用该原理进行正态分布检验。

scipy.stats.normaltest(X)

该函数输出两个结果，第一个为检验统计量，第二个为p值。如果p值大于0.05（常用显著水平）即可认定总体服从正态分布。

使用偏度和峰度拟合优度检验的还有Jarque–Bera检验法。其统计量为

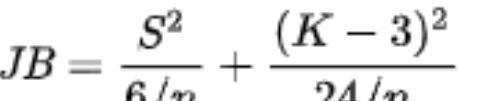
S为偏度，K为峰度，n为样本数或自由度

同样，Jarque–Bera检验样本数量也需要8个以上。其使用方法如下：

scipy.stats.self_JBtest(X)

该函数输出两个结果，第一个为检验统计量，第二个为p值。如果p值大于0.05（常用显著水平）即可认定总体服从正态分布。

2.Kolmogorov-Smirnov检验

Kolmogorov-Smirnov检验用于比较一个频率分布f(x)与理论分布g(x)或者两个观测值分布的检验方法。其原假设H0:两个数据分布一致或者数据符合理论分布。D=max| f(x)- g(x)|，当实际观测值D>D(n,α)则拒绝H0，否则则接受H0假设。D(n,α)为自由度为n，显著水平为α时的统计量阈值。

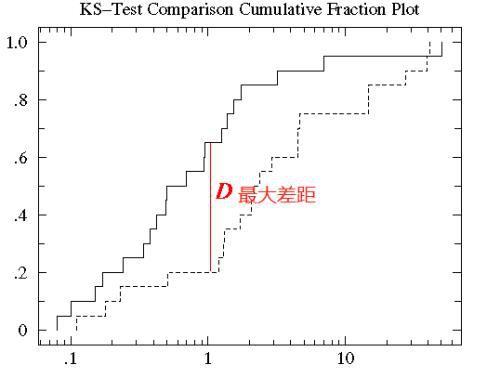
K-S检验原理

KS检验与其他方法不同是KS检验不需要知道数据的分布情况，是一种非参数检验方法，理论上可以检验任何一种分布情况（不限于正态分布检验）。当然付出的代价就是灵敏度没有专门针对某种分布的检验方法高（比如上面的normaltest）。另外，由于大多数KS检验软件在实现是都用大样本近似公式，因此KS算法更适合大样本（300以上）检验。

以下方法就是使用KS检验进行正态分布检验：

kstest(X,)

该函数输出两个结果，第一个为检验统计量，第二个为p值。如果p值大于0.05（常用显著水平）即可认定总体服从正态分布。

顺便说一下，Kolmogorov大神在统计学界可是个里程碑式的人，1933年，他出版了《概率论基础》一书，建立了概率论公理结论，这是一部具有划时代意义的巨著，困扰统计学界几百年的概率论基本定义的问题得以解决。当然他的贡献涉及到数学的所有领域，可以说是20世纪最杰出的、最有影响的数学家之一。

柯尔莫果洛夫 (Andrey Nikolaevich Kolmogorov,1903.4.25-1987.10.20)

3.Shapiro-Wilk检验

Shapiro-Wilk检验由S.S.Shapiro与M.B.Wilk提出，常简称为Shapiro检验（偶被称为W检验），专用于正态分布检验（8<样本量n<50）。该方法将样本顺序编排，然后根据以下公式计算统计量W的值，该值越接近于1，且显著水平大于0.05时，就可以接受样本所属总体服从正态分布的假设。

以下方法就是使用Shapiro检验进行正态分布检验：

scipy.stats.shapiro(X)

该函数输出两个结果，第一个为检验统计量，第二个为p值。如果p值大于0.05（常用显著水平）即可认定总体服从正态分布。

4.Anderson-Darling检验

Anderson-Darling检验，简称Anderson检验。可以检验样本数据是否服从&39;, &39;, &39;, &39; or &39;分布，是KS检验的增强版，也是一种非参数检验。适合于大样本（大于300）的总体分布检验。与KS检验相比，Anderson检验度量经验累积概率和理论累积概率之差的方法显得更加自然，考虑了所有的差异点，而不是像K-S检验那样只考虑一个最大的。下面的公式就是其方法：

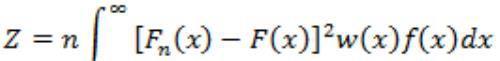
以下方法使用Anderson检验进行正态分布检验：

scipy.stats.anderson(x, dist=&39;)

其输出结果较为复杂，如：

AndersonResult(statistic=0.68097695613924714,

critical_values=array([ 0.555, 0.632, 0.759, 0.885, 1.053]),

significance_level=array([ 15. , 10. , 5. , 2.5, 1. ]))

第一个值为统计量，第三个值为显著水平百分数，第二个值为不同显著水平下的阈值。如果统计量小于某项阈值，则表示在对应显著水平下可以判定总体服从正态分布。

如上例，说明在0.05,0.025,0.01水平下，可以判定总体服从正态分布，而0.15,0.1显著水平下，不能确定总体是否服从正态分布。

5.lilliefors检验

Lilliefors检验将KS检验改进为专门的正态分布检验。它用样本均值和标准差代替总体均值和标准差，来估计样本的总体是否服从这两个参数确定的正态分布，这就是所谓的Lilliefors正态性检验。在很多统计软件中通常采用这种方法。由于该检验方法基于KS检验，因此可用于较大样本的正态性分析（样本数量50以上300以内）。

以下方法使用Lilliefors检验进行正态分布检验：

statsmodels.stats.diagnostic.lilliefors(X)

该函数输出两个结果，第一个为检验统计量，第二个为p值。如果p值大于0.05（常用显著水平）即可认定总体服从正态分布。

6.Ryan-Joiner 检验

Ryan-Joiner检验通过计算数据与数据的正态分值之间的相关性来评估正态性。如果相关系数接近 1，则总体就很有可能呈正态分布。Ryan-Joiner 统计量可以评估这种相关性的强度；如果它未达到适当的临界值，您将否定总体呈正态分布的原假设。此检验类似于 Shapiro-Wilk 正态性检验。

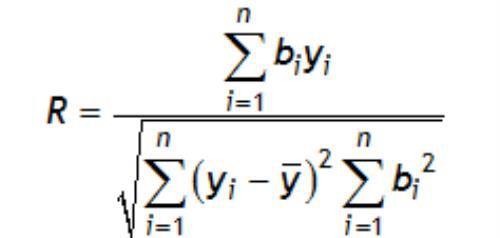
Ryan-Joiner检验统计量

该检验目前笔者还没有找到python版的软件包，日后找到再介绍给大家。

7.QQ图可视化检验

QQ图通过把测试样本数据的分位数与已知分布相比较，从而来检验数据的分布情况。利用QQ图鉴别样本数据是否近似于正态分布，只需看QQ图上的点是否近似地聚集在一条斜率为正的直线附近。如果是则说明是正态分布，该直线的斜率为标准差，截距为均值。绘图原理参看下图。

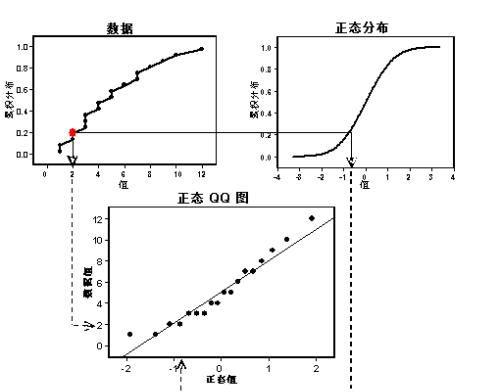
QQ图绘制过程

以下方法可以根据样本数据绘制qq图。

import statsmodels.api as sm import pylab sm.qqplot(X, line=&39;) pylab.show()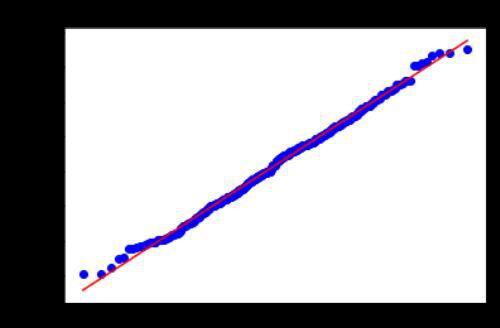

散点集中在对角线附近，可接受样本整体服从正态分布

用以下方法同样可以绘制QQ图。

import matplotlib.pyplot as pltimport scipy.stats as statsstats.probplot(X, dist=, plot=plt)plt.show()

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小海创作整理编辑！