幂级数收敛域的求解方法有几种(幂级数收敛域和函数怎么求)

导语：高等数学之幂级数收敛域和和函数问题方法总结

幂级数是考研数学的重点考察的知识点，数学一基本上每年都考级数这一章的知识。幂级数这一章大题的考点主要有如下两个：

（1）幂级数的收敛域及和函数；

对级数这一章，数一的同学要将幂级数的和函数作为重点知识来复习，考研中幂级数的和函数的 考题最多。幂级数的和函数又分为先导后积、先积后导。两种方法大家都要掌握。

幂级数收敛半径：

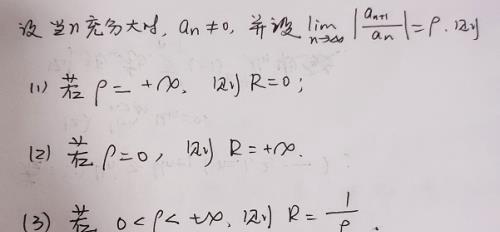
幂级数收敛半径计算方法

（2）幂级数的展开式；

幂级数的分析性质：

常用函数的麦克劳林公式：

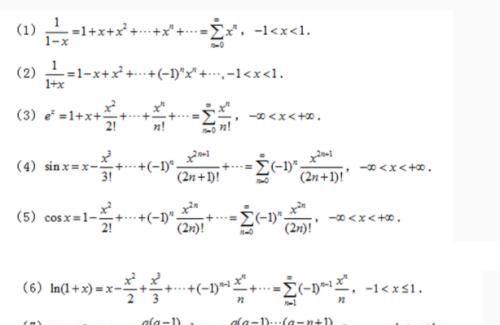
题型一：求幂级数的收敛域

方法总结：先求收敛半径，然后再判定在端点出幂级数的敛散性，便可求得收敛域。

例1：求下列幂级数的收敛域。

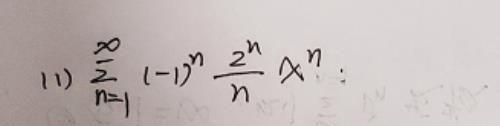
解：

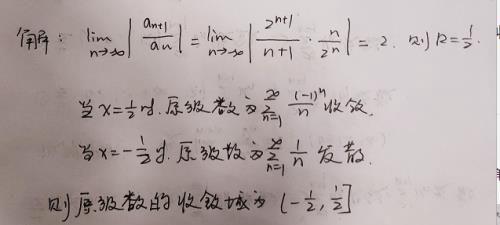
题型二：求幂函数的和函数

常用方法如下：

（1）常见的麦克劳林公式；

（2）幂级数的逐项可导性和逐项可积性；

（3）求幂函数满足的微分方程，求解微分方程；

常用的技巧如下：

例2：求下列幂级数的和函数

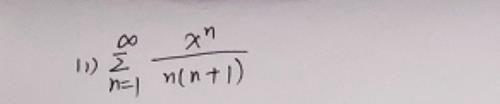
分析：充分利用常用的麦克劳林公式进行求解

解：

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小蔼创作整理编辑！