如何分析异质环境下各向异性扩散对图灵斑图的影响?
导语:如何分析异质环境下各向异性扩散对图灵斑图的影响?

文丨煜捷史馆
编辑丨煜捷史馆


扩散是一种非常普遍的物理现象,它可以用来描述从高浓度区域到低浓度区域的物质传输,扩散在自然界中无处不在,从人体内的细胞到大气中的气体,都可以通过扩散来传输物质。
在异质环境中,扩散通常表现出各向异性,各向异性扩散是指在不同方向上的扩散速率不同,各向异性扩散在许多自然系统中都是非常重要的,例如,大气中的气体扩散、地球内部的物质扩散以及生物体内的物质传输。
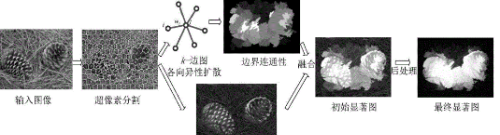
在生物体内,扩散是一种非常重要的生物物理学过程,通过扩散,细胞可以传输营养物质和代谢产物,在生物体内,扩散往往发生在异质环境中,例如,细胞内的细胞器和膜具有不同的物理和化学性质,这种异质性环境会影响扩散的速率和方向,因此,在异质环境中研究扩散的行为对于理解生物体内的物质传输和化学反应具有重要意义。
图灵斑图是一种描述各向同性扩散行为的图像,它通常被用来描述非线性反应扩散系统中的空间结构,然而,在异质环境下,各向异性扩散会影响图灵斑图的形状和大小,因此,在本文中,我们将研究异质环境下各向异性扩散对图灵斑图的影响。
我们使用数值模拟方法来计算在不同强度和方向的各向异性扩散下,图灵斑图的变化,通过这项研究,我们可以更好地理解生物体内扩散的行为和在异质环境下的应用。

 理论基础
理论基础1各向异性扩散张量的定义和性质
各向异性扩散张量是一种描述物质在各个方向上扩散特性的张量,它反映了物质在不同方向上的扩散速率和扩散方向,在均匀介质中,各向同性扩散张量具有相同的元素,因为物质在任何方向上的扩散特性都是相同的,但在非均匀介质中,物质在不同方向上的扩散特性可能会不同,因此需要使用各向异性扩散张量来描述。
各向异性扩散张量的性质与其对应的物质的晶体结构、形态和各向异性分布有关,例如,如果物质的分子结构呈现出一定的对称性,则其各向异性扩散张量也具有相应的对称性质,此外,各向异性扩散张量也与物质分子的形态有关,例如,某些分子的扩散速率在不同方向上可能会受到其形态的限制,因此其各向异性扩散张量也会相应地呈现出不同的性质。
各向异性扩散张量的性质对于研究物质在非均匀介质中的扩散行为具有重要意义,通过测量各向异性扩散张量和分析其性质,可以更加深入地了解物质在不同方向上的扩散行为,以及其在异质环境下的传输特性,此外,各向异性扩散张量的研究还有助于设计新型材料,改进现有材料的性能,并开发出更加高效的分离和过滤技术。

2图灵斑图的定义和计算方法
图灵斑图(Turing pattern)是由英国数学家阿兰·图灵(Alan Turing)在1952年提出的一个重要的自然界模式形成理论,它是指当化学反应在均匀环境中发生时,由于反应扩散耦合作用,会出现自组织的斑纹和图案,这些图案可以在非线性反应扩散方程中产生。
图灵斑图所对应的方程包含非线性反应和扩散项,并且在系统的某些参数范围内,可以引起反应物浓度在空间中的局部不均匀性和自组织出多种斑纹和图案。

计算图灵斑图的方法通常基于有限差分法或有限元法的数值模拟,在数值模拟过程中,需要首先确定一个反应扩散方程,然后对方程进行离散化,最后使用时间积分方法求解,离散化的过程中需要对各向异性扩散张量进行处理,以考虑系统中存在的各向异性情况,时间积分方法通常使用显式或隐式的欧拉方法,或者基于二阶或四阶龙格-库塔方法等。
计算完毕后,可以通过分析模拟结果的图像,确定图灵斑图的形态和特征参数,这些特征参数包括斑纹的周期、大小、形状、对称性等,同时还可以进行对比分析,以研究各向异性扩散对图灵斑图的影响,探讨图案形成机制的物理本质。

 数值模拟方法
数值模拟方法1有限差分法或有限元法的基本原理
有限差分法(Finite Difference Method,FDM)和有限元法(Finite Element Method,FEM)是数值模拟中常用的两种离散化方法,在实际应用中,通常需要将偏微分方程转化为离散形式,然后用计算机进行求解,得到近似的解,其中,有限差分法是最早被发展的数值离散化方法之一,也是最为简单易用的方法之一。
其基本思想是将空间离散化为有限个节点,将时间分段离散化,然后在离散点处对偏微分方程进行数值逼近,最终得到近似解,在有限差分法中,空间上的导数用节点处的函数值差分逼近,时间上的导数用前后两个时间步之间的函数值差分逼近。
根据所选的差分格式不同,可以得到不同精度和稳定性的数值解,有限差分法的优点是简单易懂,计算速度快,但其精度和稳定性往往受到网格尺寸和时间步长的限制。
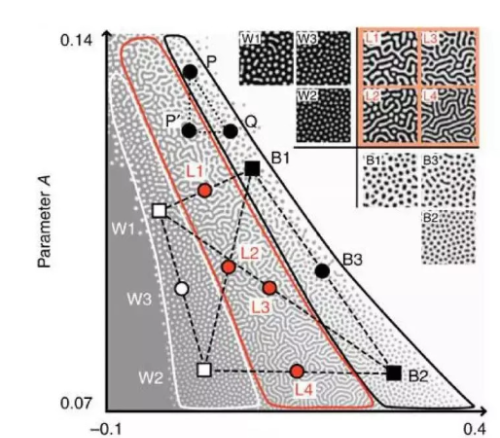
相比之下,有限元法则是一种更为通用和灵活的数值离散化方法,它将物理问题的连续域离散化为一组有限个小区域,即有限元,每个有限元由一组简单的几何形状(如三角形或四边形)和节点组成,可以用来逼近原始偏微分方程。
在有限元法中,首先需要将物理问题的偏微分方程转化为变分形式,然后将其用有限元函数的线性组合来逼近,其中,有限元函数通常是简单的多项式函数或三角函数,有限元法在数值离散化中的灵活性和通用性,使其成为目前最受欢迎的数值模拟方法之一。
然而,相较于有限差分法,有限元法需要进行更为复杂的数学推导和程序实现,计算量较大,同时,其精度和稳定性也往往受到网格尺寸和元素尺寸的影响。
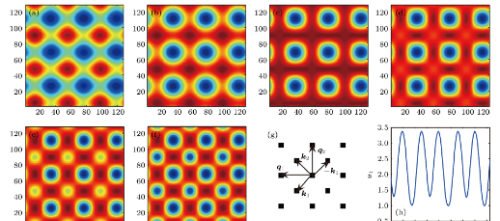
2各向异性扩散情况下的离散化方法
各向异性扩散是指在不同方向上扩散系数不相等的情况下,扩散现象的发生,对于反应扩散方程,为了能够模拟各向异性扩散的情况,需要对其进行离散化处理,一种常用的方法是有限差分法,其基本思想是将空间和时间连续的问题转化为离散的问题,通过差分代替微分运算,从而求解方程。
在各向异性扩散情况下,有限差分法的离散化方法需要对不同方向上的扩散系数进行处理,一种常用的方法是在网格上引入斜交坐标系,根据各向异性扩散系数的不同,对坐标系进行旋转和伸缩变换,从而得到在新的坐标系下的扩散系数。
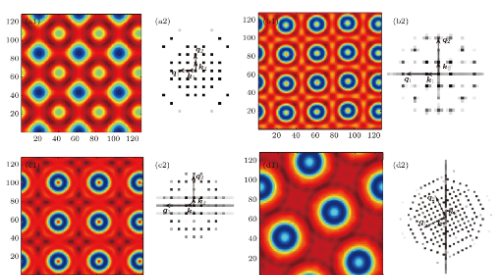
然后根据扩散系数在新坐标系下的值,对方程进行差分处理,得到一个系数不再恒定的离散化方程,这个离散化方程可以用解耦的迭代法或者代数多重网格方法求解。
另外,还有一种常用的离散化方法是有限元法,在有限元法中,可以根据各向异性扩散系数的不同,选择合适的有限元函数空间,以满足扩散方程的各向异性,有限元法的离散化方法相对于有限差分法而言,更具有灵活性和通用性,可以用于处理各种不规则几何形状的问题。
各向异性扩散情况下的离散化方法是为了模拟现实问题中扩散现象的各向异性而设计的,主要应用于有限差分法和有限元法等数值模拟方法中,对于不同的问题,可以根据具体情况选择合适的离散化方法来解决。

3时间积分方法
时间积分方法是求解偏微分方程(PDE)时间演化的一种数值方法,偏微分方程的解是随时间和空间变化的,时间积分方法将时间分割为若干个离散时间步,然后通过对每个时间步进行离散化,将偏微分方程转化为一个数值计算问题,从而得到PDE的数值解,常见的时间积分方法有Euler方法、Runge-Kutta方法、Crank-Nicolson方法等。
Euler方法是一种最简单的时间积分方法,它的基本思想是用当前时间的数值解逼近下一个时间的解,即将时间区间离散化为一系列的时间点,然后用当前时间点的解来计算下一个时间点的解,这种方法简单易懂,但是数值误差较大,不太适用于求解高精度问题。

Runge-Kutta方法是一种较为常用的时间积分方法,它利用中间点的数值解来逼近当前时间点和下一个时间点的解,它的精度比Euler方法高,但计算量也更大。
Crank-Nicolson方法是一种隐式的时间积分方法,它在当前时间点和下一个时间点之间,同时考虑这两个时间点的解,从而得到更为稳定的数值解,这种方法的计算量较大,但精度较高,因此在求解精度要求较高的问题时较为常用。
时间积分方法在求解偏微分方程的数值解时发挥着重要的作用,但不同的时间积分方法适用于不同类型的问题,需要根据具体问题的特点,选择合适的时间积分方法,以获得较为准确和稳定的数值解。

4数值模拟程序的实现
数值模拟程序的实现是本研究中非常重要的一步,我们采用了有限差分法来离散化反应扩散方程,同时考虑了各向异性扩散的情况,在数值模拟中,我们需要将模拟区域离散成小的网格,并在网格上计算方程的解。
离散化过程中,我们使用中心差分方法来计算反应扩散方程中的二阶空间导数项,这个方法可以得到较高的精度,对于各向异性扩散的情况,我们将扩散张量分解为正交矩阵和对角矩阵的乘积形式,并分别在各个坐标方向上计算方程的解。

同时,我们还需要对时间进行离散化,采用显式欧拉方法进行时间积分,在程序实现过程中,我们需要注意各向异性扩散情况下的网格剖分,以保证计算结果的准确性,我们采用了C++语言编写程序,并使用MPI并行计算技术来加速程序的运行。
最终,我们可以得到各向异性扩散情况下的图灵斑图模拟结果,从而分析各向异性扩散对图灵斑图形态和特征参数的影响。
