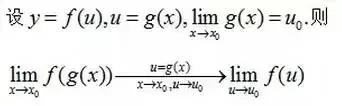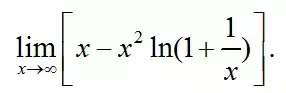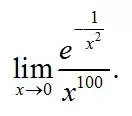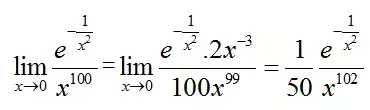变量代换的意义(变量代换的特殊技巧)

如果非要从众多的极限计算方法中

选一个最常用的出来

相信很多同学都会毫不犹豫的选择

洛必达法则

而很少使用泰勒的

而此时，我想泰勒此时的心情应该是这样的

事实上

在研究生考试当中

若能把洛必达适时的晾在板凳上

并能熟练的运用泰勒公式进行极限计算

这才算达到了至高境界

当然

除了泰勒跟洛必达

还有很多童鞋会选择

两个重要极限跟等价无穷小

等等等等

但，很少会有同学选择

变

量

代

换

事实上，在极限计算当中，变量代换简直牛逼的一塌糊涂。

能够将变量代换和其他极限计算的方法联合起来，更能发挥其无穷的威力...

试想一下，当你在在山穷水尽、一筹莫展、江郎才尽、黔驴技穷之时，根据具体题目做出合适的变量代换，往往能化腐朽为神奇，峰回路转、柳暗花明、人见人爱、花见花开…

（小伙伴们表示：我类个去，神马乱七八糟的）

废话说了那么多

总之一句话：

我们先来了解一下变量代换的表达式：

例题1. 求

此时，小伙伴们的思路一定是：这是这是

型的未定式，一般做法是通分，将其转化为 0/0 型.然后放洛必达收拾这个小婊砸。

不对，这TMD根本没有分母，如何通分。

看官莫慌，请听小编一言，我们可以利用变量代换创造出个分母。从而化腐朽为神奇。

是不是，很神奇，很好用，用一次想两次，用两次想三次。用了还想用，

没想到小伙伴们有这种癖好，小编我就满足你们把。

例题二，求

乍一看，0/0型的未定式，看起来好简单。放洛必达。

然后

......

纳尼好像哪里不对了。用了一次洛必达好像比原来的更难了！

如果一上来就使用洛必达，你就中了出题人的诡计了！

看官莫慌，请再听小编一言，我们可以利用变量代换，转化为我们熟悉的形式。从而再次化腐朽为神奇。

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小里创作整理编辑！