微分几何中的测地线浅谈

“测地线”是微分几何学中最重要和最基本的概念之一，也是几何学最基本的研究对象。测地线的研究不仅推动了几何学的发展，实际上很多物理定律及现象也可以通过测地线的相关结论来合理解释。那么，什么是测地线，它又有怎么的性质呢？

测地线(Geodesic)一词最早不属于几何这个学科，而是来自大地测量学(Geodesy)，这一点我们从它的名字大概就能看出来。伟大的数学王子高斯，曾经主持过一项浩大的工程，那就是为汉诺威王国绘制详细的地图，为此他耗费大量时间实地测量，之后利用最小二乘法等数学方法处理相关数据，极大地提高了地图精度。在这个过程中，测地线就是高斯经常遇到的数学对象。

我们先从最简单的欧式空间说起，这种情况下的测地线有非常好的几何描述，那就是它是连接两点的最短路径，也就是我们非常熟悉的直线段，从严格的数学角度来说，这正是直线段的定义。欧式空间上的测地线的确平淡无奇，没有什么好研究的，但当空间的形状改变时，情况就没有这么显然了。

例如球面，我想很多人都并不知道球面上的测地线是什么样的，即使知道可能也不清楚背后严格的数学系证明。可能很容易猜得到连接球面两点之间的最短路径位于过球心的大圆上，但要非常严格地说明这件事却并不太容易。而且为了更好地获得测地线的信息，我们必须要有更为一般的理论，以便分析更为复杂的空间。

为此我们要先简单介绍一下曲线的测地曲率。测地曲率有非常形象化的解释：

对于曲面S中的曲线C，它在曲面S的P点处切平面上会产生一条投影曲线，而原曲线C的测地曲率就等于投影曲线的相对曲率。

利用测地曲率，我们就可以得到曲面上测地线的定义：

曲面上测地曲率恒为0的曲线成为测地线。

但这样定义出来的曲线还会是连接任意两点的最短曲线吗？事实上，测地线包含所有曲面上的最短曲线，而且会往往超出这个范围，也就是说，最短曲线一定是测地线，但测地线不一定最短。产生这种现象的原因在于我们仅仅使用曲率，或者说曲面的度量来定义测地线，但曲线的最短性并非一个像高斯曲率那样的内蕴几何量，因而就无法保证最短性。还是以球面的大圆为例，对于大圆弧上的非常接近的两点，连接它们的优弧和劣弧都是测地线，但显然只有只有一条是最短的。

进一步的研究表明：

测地线一定是局部最短的！而局部的意思就是说测地线上两个点充分接近，例如球面大圆上的两个点如果很接近，那么就可用较短的圆弧连接。

系统地建立起关于测地线的理论之后，我们才能对它的性质有更深刻的理解。我们显然可以看到的是，有了微分几何的方法后，寻找曲面任意两点的最短路径才变得容易，对于那些不规则或难以想象的曲面而言，测地线是几乎无法凭空想出来的，例如双曲面和抛物面等等。

对于曲面而言，还有一个关键的问题，那就是是否曲面上的任意两点都有最短曲线相连呢？答案显然是否定的，例如去掉球面大圆上的一个点，那么大圆上此点前后比较接近的两个点就无法取到最短路径。这样的曲面我们称之为不完备曲面，反之，若任意二点有最短测地线相连，那么就称之为完备曲面。完备的空间是微分几何中非常重要的一类研究对象，判断一个空间是否完备也是重要的研究课题。

测地线这种具有极小性质的数学对象，从一开始就是変分学的重要研究对象，而変分学的目的就是要从一大类函数空间中找到具有极值性质的那一个，例如著名的最速下降问题，牛顿利用変分的思想最早证明了此时的物体下降轨迹为悬链线。对于曲面上的两点，连接它们的曲线往往有无数条，寻找极短测地线于是就可以转化成一个変分问题，这时就有了弧长第一变分公式。如同研究微积分中的函数极值那样，一阶导数为零一般只是函数取极值的必要不充分条件，我们需要计算它的黑塞矩阵来判断函数到底取没取到极值，在这样的思想的推动下，我们又得到了弧长的第二変分公式。

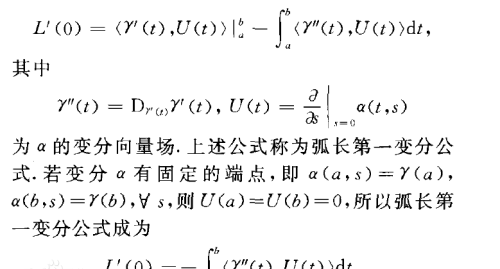
测地线的重要性体现在它不仅仅是弧长変分的极值点，很多情况下也是能量変分的极值点，于是我们可以用来解释为什么光在我们所处的均匀空间中是沿直线传播的，此时它所带有的能量最小因而更稳定，这也是符合物理中最小作用原理的。牛顿第一定律描述的也是这样的原理，如果物体不受外力作用，为了保持能量最小，那么它只能静止或一直沿直线匀速运动。可以说，测地线是変分法和最小作用原理的极佳范例。

所以我们可以设想，如果宇宙中存在某处像球面的二维空间，那么那里的“匀速直线运动”实际上是沿大圆周运动。

对于高维的欧式空间，测地线的性质同样会保持正确，而且自从黎曼推广了高斯的内蕴几何，创立黎曼几何以来，测地线的概念不仅得到了相应的推广，而且同样在新的几何学中发挥着极为关键的作用。同时，测地线的概念还有了高维的推广，测地线是弧长和能量变分的一维解，而如果我们考虑高维解，那么就有了极小曲面的概念，实际上这也可以解释为什么我们吹的泡泡是球面，因为球面就是典型的极小曲面，携带的能量最小，更稳定，同时在给定条件下，极小曲面往往也是面积最小的一个，这和测地线是相似的。当然，这些概念在数学上有更为一般和精确的定义，往往并不局限于它们的物理意义，但这里我们就不展开讨论了。