代数学是数学中最古老的的学科之一，在之后相当长的一段时期内，代数学都曾成为数学的中心。但中世纪过后，传统的代数学开始沉寂，陷入解方程的泥淖中，而自微积分被发明之后，数学迎来分析学的黄金时代，进而代数学的地位一度岌岌可危，这样的局面一直持续到19世纪初。进入19世纪后，代数学在众多数学家的努力之下，终于获得解放，重获生机，再次成为数学的中心学科之一 。此时，代数朝着两个大方向阔步前进，一是由解方程理论所发展出来群论和域论等，代表性数学家有伽罗瓦和阿贝尔等，而第二个大方向则是研究代数本身的内在逻辑与性质，我们今天所介绍的“四元数”便是这一方向的代表性成就。

复数

我们都知道16世纪数学最伟大的成就无疑是彻底解决了三次和四次代数方程的求解问题，而卡尔达诺(Jerome Cardan，1501—1576)则是这一过程中的关键人物。为了求解方便，他引入了虚数和复数的概念，但自此之后一两百年间，复数却成了数学家的心头大患，因为没有人能清楚地说明复数到底是个什么东西，关于它的运算又是否合理。直到复数可以用来解释平面向量的运算后，它才在直观上普遍被数学家们所接受。而在1837年，爱尔兰著名数学家和力学家哈密顿将复数解释为满足一定条件实数的有序对，避免了当时还含糊不清的虚数的使用。简单来说，把两个复数a+bi和c+di分别记为(a,b)和(c,d)，那么它们应满足:

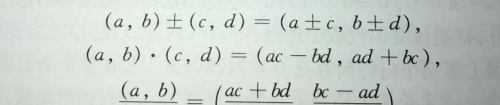
按照这样的解释，复数就成为了满足交换律，结合律和分配律等性质的代数体系。但即便如此，复数的几何作用仍是数学家乃至物理学家所关注的重点，因为向量实在是太好用了。关于这一点，哈密顿本人也是十分赞同的，有意思的是，以后人的眼光来看，哈密顿更广为人知的贡献却集中在物理领域内，而非数学。

哈密顿

说到这里，我们还是要简单介绍一下哈密顿，哈密顿(William Rowan Hamilton 1805～1865)出生于爱尔兰都柏林，是爱尔兰历史上最伟大的数学家，就数学而言，在英国及爱尔兰地区的历史地位仅次于牛顿。哈密顿的主要物理贡献集中在几何光学以及分析力学，学过相关课程的人应该都清楚他的巨大成就。但从本质上说，哈密顿无疑是数学家，因为这些成就都非常“数学化”，甚至可以看做是数学在物理中的应用。而哈密顿在纯数学上最大的贡献无疑就是大名鼎鼎的“四元数”。

在提出四元数之前，哈密顿和许多数学家都曾致力于寻找“三维复数”，目的则是为了把平面向量的性质平行地推广到三维空间中，以便为三维空间中的力学等学科找到理想的数学工具。伟大的高斯也曾思考过这个问题，他提出过一种“三维复数”的代数体系，但必须抛弃掉结合律，而这种代数却不符合实际需要，后来就无人问津了。致力于此的哈密顿在多年寻找以后，也不得不宣告这项计划的破产，但哈密顿的高明之处在于，他没有恪守成规，而是去寻找新的突破口。

多年思考和尝试后，哈密顿意识到三维空间中可能并不存在完全类似于平面复数那样的代数体系，于是他将目光转移到了四维空间，但不久之后他还是发现似乎四维空间中也没有完美的代数体系。回想起高斯的“三维复数”后，哈密顿意识到可能必须要牺牲掉某些过于严格的要求，而且关键在于如何定义“四元数”的乘积使得这个代数体系自洽。

哈密顿最终灵光一闪，成功构造出“四元数”的故事流传得相当广泛，但与很多没有根据，以讹传讹的数学故事不同，哈密顿和四元数的最终故事是完全真实的，这可以由他自己写的回忆佐证。1843年的10月16日，哈密顿和夫人散步来到一座桥时，他驻足思考良久，突然间幸运女神降临，哈密顿想清楚了四元数乘法定义的所有关键细节。兴奋不已的哈密顿赶紧拿出随身携带的笔记本将细节写下来，四元数便这么诞生了！

哈密顿发表于1858年的回忆

四元数

四元数的基本形式为a+bi+cj+dk，a,b,c,d为实数，a为数量部分，bi+cj+dk为向量部分，其中的i,j,k类似于虚数。它们之间的加法完全和复数一样，而定义i,j,k的乘积法则如下：

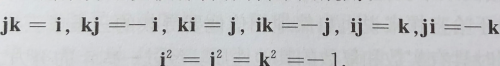
在这样的规定之下，四元数成为一个非交换的结合代数。四元数的问世极大地震撼了当时的数学界，原因就在于它的非交换性，交换性在数学家的眼中是代数的固有性质，而这样的非交换代数的横空出世冲垮了许多人的心理防线。哈密顿本人对这个来之不易的四元数极其珍视，认为它将和微积分一样在数学和物理中发挥重要的作用。哈密顿身先士卒，利用四元数，他先后定义了如今我们熟知的梯度，散度和旋度等微分算子，并且应用到物理中去。

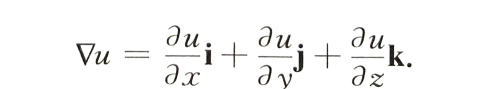
梯度算子

向量分析与结合代数

四元数就像一枚重磅炸弹在科学界炸开，直接导致支持派和反对派的对立，在哈密顿提出四元数后的几十年里，由于它的实用性还比较有限，许多物理学家宁愿使用原来的笛卡尔坐标而放弃四元数。但后来还是有人发现了四元数的巨大潜力，这就是伟大的麦克斯韦(James Clerk Maxwell,1831〜1879,英国著名物理学家，经典电动力学和统计物理奠基人)。结合自己的研究工作，麦克斯韦洞察到了哈密顿的局限，那就是他往往整个地使用四元数而不区分数量和向量部分。麦克斯韦在独立使用四元数的数量和向量部分后，把哈密顿原先所定义的散度等概念应用到向量函数上，并且还重新定义了一个新的微分算子，也就是拉普拉斯算子。

麦克斯韦

这样强有力的数学工具在麦克斯韦的电磁学研究中起到了重要作用，这直接体现在了他非常著名的麦克斯韦方程组当中。麦克斯韦的工作真正展现了四元数的巨大作用，表明了它可以发挥的作用绝不仅仅是使得计算更方便而已，而在此基础上则发展出了“向量分析”这一全新的数学学科。

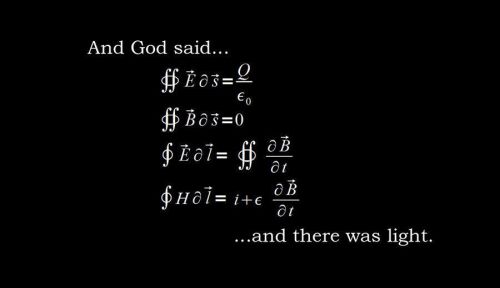
麦克斯韦方程组

与哈密顿同时代的另一位数学家格拉斯曼(Hermann Gunther Grassmann,1809～1877)也在进行推广复数的工作，他的工作即所谓的“线性扩张论”，特别地，格拉斯曼定义出了向量的内积和外积等概念，所产生的结果在许多方面和哈密顿的四元数相关联。尽管格拉斯曼也致力于将“超复数”的成果应用到物理中去，但由于格拉斯曼的研究独创性太强且叙述语言又晦涩，以致于同时代的数学家基本上都无法接受他的成果。

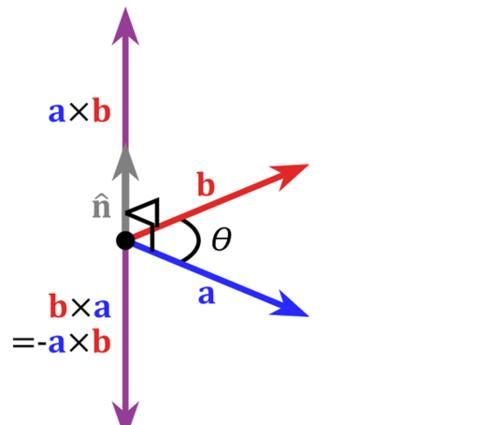
向量外积

到了19世纪80年代，四元数的第一个正式副产物开始诞生，这就是三维“向量分析”，而且准确来说，“向量分析”是四元数向量部分所引出来的，这些是由吉布斯和赫维赛共同发展起来的。吉布斯(Josiah Willard Gibbs，1839~1903)是美国耶鲁大学的数学物理教授，也是著名的物理化学家，学过化学的同学可能都听说著名的“吉布斯现象”，而且此吉布斯正是彼吉布斯，实际上吉布斯是数学，物理和化学三方面的全才。赫维赛(Oliver Heaviside，1850~1925)的名气同样也不小，他在电磁学及其应用上都做出过杰出贡献，将麦克斯韦方程组改写成了如今的模样，而且提出了著名的赫维赛函数。

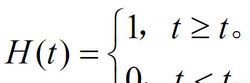
赫维赛函数

吉布斯和赫维赛所发展的向量分析中定义了两种不同的乘积，即内积和外积(又称向量积)，但它们都与四元数中的乘积有所不同，在内积下向量构成一个可交换而不可结合的代数，而在外积下，向量既不可交换也不可结合。两种乘积下的向量分析都在物理和数学中发挥了巨大作用，例如它们可以用到电磁学，流体力学，解析几何和微分几何等学科。

同时，四元数也推动了数学家去寻找更多满足不同定律的代数系统，这其中著名的还有凯莱的八元数和克利福德的拟四元数，矩阵论兴起后，人们也发现矩阵在矩阵乘法下构成一个不可交换的结合代数，而这应用到物理中又促进了矩阵力学的诞生。赫维茨最终在1898年证明了一个重要的结论，算是在19世纪末给这个经典问题画上了圆满的句号：

满足乘法定律的线性结合代数仅有实数，复数，哈密顿四元数以及克利福德拟四元数。

直到20世纪，研究各种各样满足不同定律的代数都仍然是一个重要的课题。

结语

在哈密顿的四元数问世不久后，热力学之父开尔文曾不怀好意地说过：

向量是无用的幸存物或四元数的无价值支流，对任何创造，从未发挥过哪怕是最细微的实际作用……

但之后几十年四元数及向量所发挥的巨大作用绝对是当时的开尔文想不到的，而且他的“打脸言论”在多年之后再次上演，也就是我们今天津津乐道的“物理中的两朵乌云”。从数学的长远发展来看，要提出革命性的新事物往往会遭遇巨大的阻力，例如罗巴切夫斯基的非欧几何，伽罗瓦理论，勒贝格的实变函数论等等，但事实证明，真理无论被埋没多少年都会最终散发它的耀眼光芒。当回溯今天所介绍的内容后，我们都应发现，哈密顿和他的四元数就是这一切的源头。