法国数学家韦达和符号代数

代数学是数学中最古老的的学科之一，从最早的整数，有理数，到方程，再到群环域，最后到如今各种各样的代数体系，代数学这个学科几经兴衰后才发展如今这样的数学主流学科。那么代数学发展过程中最重要的节点是什么呢？我们从整个数学发展的历史来看，符号代数的出现无疑是一件不可或缺的里程碑事件，而符号代数的关键人物正是我们中学生都知道的被誉为“符号代数之父”的法国数学家韦达。

韦达(François Viète,1540~1603)出生于法国普瓦图地区的一个贵族家庭，他早年的职业是律师，这一点和费马很像，实际上我们可以发现，很多当时的数学家都当过律师，这是因为律师是最体面的工作之一，贵族子弟中有能力的人中很多都会选择从事这一职业。后来韦达走上仕途，在政府部门出任议员等职。但数学一直是韦达的“业余爱好”，为此他花费了几乎所有闲暇时间，实际上在韦达的时代，还没有出现专职的数学家。

在韦达之前，数学家们基本是沿用被称为“代数学之父”的古希腊数学家丢番图(Diophantus)所留下的代数符号体系，即使后人有所改进，也只不过是将单词缩写而已，加减这样的运算符号也只是用字母代替，这一局面一直持续到16世纪初。到了韦达的时代，为了数学的有效发展，一些数学家有了以符号代替词语的意识，但一直都不成体系，而韦达则是历史上第一个有意识而且系统使用字母和符号的数学家。

韦达的习惯是用辅音字母表示已知数而用元音字母表示未知数，而用拉丁语表示数的指数，例如a^2他记作a quadratum。尽管韦达明确地使用了“+”和“-”的运算符号，但却没表示乘法和相等的符号，而仍是用拉丁语表示，例如他将

a^3+3a^2b+3ab^2+b^3=(a+b)^3

记作

a cubus+b in a quadr. 3+a inb quad. 3+b cubo aequalia a + b cubo.

这些都说明，韦达的符号体系还是不全面的，后来经过许多数学家的完善才形成了我们今天的体系，例如笛卡尔明确地以字母表前面的字母a,b,c等表示已知数或方程的系数，而已字母表最后的x,y,z等表示未知量或方程未知数，这样的习惯被沿用至今。

有了符号体系后，一些传统的代数知识才开始成为系统。三次和四次代数方程的求解是16世纪最重大的数学成就之一，但在韦达之前，数学家往往只能针对各种类型的方程求解，例如卡尔达诺在他著名的《大法》一书中所涉及的方程高达66种，而每一种都有特殊的解法，这无疑徒增学习和传播数学的压力。韦达用自己的符号系统改写了前人的解方程方法，直接用含系数的代数式将解表示了出来，他还顺便得到了如今我们熟知的关于方程根系的“韦达公式”。对于二次和三次方程的韦达公式，韦达本人给出了证明，同时，他也给出了一般n次方程的韦达公式，但他没能证明，这样的证明直到两百年后，在高斯证明了代数学基本定理后才得到完全的证明。

除去方程论外，韦达在三角函数方面的贡献也非常大，例如他给出了正切定理，正弦差公式以及球面三角形的余弦公式等。令人惊讶的是，在没有微积分的时代里，他还给出了一般n倍角的正弦公式：

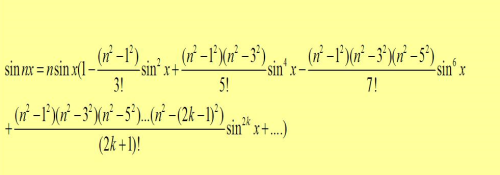
利用这个n倍角公式，韦达曾成功地解出了一个45次方程的23个根！这里我们要特别说明，在韦达的时代，还没有复数的概念，所以他得到的根只有实根。

不仅如此，韦达还给出了历史上第一个圆周率π的解析表达式：

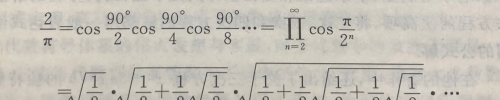
可以说，韦达是同时代里最杰出的数学家之一，他的贡献丰富，创造性强而且影响深远，尤其是他的符号体系思想深深改变了代数学的面貌，自此代数学才开始成为一门独立而系统的数学学科。韦达无愧为“符号代数之父”！