比圆周率更神秘的“混沌”常数:4.669201609102...
导语:比圆周率更神秘的“混沌”常数:4.669201609102...

这“混沌”常数
比π还要神秘
40多年前,一个实验室助手拿着一个计算器算出了一个比圆周率更神秘的常数:4.6692......,它涉及了大自然的秘密,开启了混沌现象普适性研究。
超模君今天要讲的就是这位混沌的先驱者:米切尔·费根鲍姆!

30岁前,名下只有一篇文章,曾经历过被学校辞退的他,是如何从一个默默无闻的博士成为一鸣惊人的数学物理学家?
生性古怪,被学校辞退
说到费根鲍姆,更多人想到的是获得图灵奖的爱德华·费根鲍姆,其实米切尔·费根鲍姆也应该让更多人知道。

米切尔·费根鲍姆,1944年出生在美国费城。第二次世界大战后,举家搬迁到布鲁克林定居,他的父母是来自波兰和乌克兰的犹太移民,他父亲是纽约港务局的公务员,母亲是公立学校的老师。
大概是因为父母工作忙,突然转学等原因,导致米切尔·费根鲍姆从小就比较内向,行为在外人看来比较古怪,但却十分思考,常常会有提出一些天马行空的问题。
虽然费根鲍姆生性古怪,但是他学习成绩不差,从小就立志做一名电子工程师,因为他了解到电子是热门专业,毕业后能挣钱。1964年如愿取得了纽约学院的电子工程专业的学士学位。

本科毕业后,离实现梦想仅一步之遥,费根鲍姆面临着选择,一个是能挣钱的电气工程师,很多同学都选择的路;一个是浩瀚的物理海洋。这次,他没有随大流,选择继续探索物理世界。
费根鲍姆跨专业转向物理学,进入麻省理工学院技术研究所读研,花了6年时间潜心在物理领域的热门方向基本粒子,成功取得麻省理工学院的硕士和博士学位。
虽然顺利毕业,但是让人讶异的是,费根鲍姆在硕博士期间并没有拿得出手的学术成果,30岁前只有一篇文章。那是因为大家不看好的新领域混沌理论研究深深吸引了他,让他放弃了大家认为前途一片光明的基本粒子研究。
他之所以没有学术成果,很可能是因为硕博期间就已经开始研究混沌了,那一篇文章或许是用来应付博士毕业的。

博士毕业后,费根鲍姆凭借麻省理工的博士帽子进入了康奈尔大学工作,他每天都花很多时间研究才开始出现的非线性和chaos(混沌),新领域走在前沿,很难出成果。
康奈尔大学认为这是一个暂时看不到未来的方向,更希望费根鲍姆能研究大热的基本粒子领域,而费根鲍姆对混沌的研究已经着迷,不久便被辞退了。
在同行们眼里,费根鲍姆是非常奇怪的一个人。他说话总是很快,往往丢掉冠词和代词,仿佛有点中欧腔。
后来有费根鲍姆在弗吉尼亚理工研究所工作过一段时间,他坚持对混沌研究让他的工作再次受阻,不久便离开了。这次他清楚地认识到要寻找一个能专心研究混沌相关的工作。
1974年,他跳槽到洛斯阿拉莫斯国家实验室理论部给一个教授做助手,没啥地位,工资不高。但是能研究水流紊乱这个世纪大难题,或许对混沌研究有帮助。
发现常数,被认可
虽然在洛斯阿拉莫斯实验室只谋到一个助手的职位,但是却成了他人生的转折点。
费根鲍姆所在研究小组的课题是流体力学中的湍流现象,费根鲍姆需要研究的是:威尔逊的重整化群思想是否可以解决湍流这个世纪老难题。
刚开始时,费根鲍姆并不是十分钟情于研究小组的这个课题,但因为湍流看起来一片混乱,像极了自己热衷的“混沌”,便进行了深入研究。
费根鲍姆工作时像着魔一样,甚至可以不吃饭不睡觉,无法工作时就散步和思考,无论白天还是夜晚。
这个研究方向使得费根鲍姆了解并熟悉了气象学家洛伦茨宣告的“蝴蝶效应”,以及逻辑斯蒂迭代时产生的混沌问题。
蝴蝶效应图像
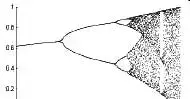
逻辑斯蒂分岔图
特别是逻辑斯蒂分岔图中出现得越来越多的那些三岔路口,让费根鲍姆非常感兴趣,他觉得这其中肯定存在着某种规律。
虽然他在洛斯阿拉莫斯实验室的地位不高,但是实验室的设备还是很先进的,他得了一个能放在口袋里的HP65计算器,一有空闲,他便一边散步、一边抽烟,不时地还把计算器拿出来编写几句程序。

现在看起来十分简易、当时售价为795美元的HP-65是惠普公司的第一台磁卡-可编程手持式计算器,用户可以利用它编写100多行的程序,还可将程序存储在卡上,对磁卡进行 读写。这在上世纪70年代已经显得很了不得,因而,HP-65的绰号为“超级明星”。
就是这个计算器,在费根鲍姆发现常数过程中,发挥了很重要的作用。他用计算器编程序算出每个三岔路口的坐标,即k值和相应的x无穷值。
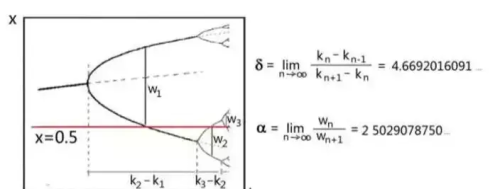
费根鲍姆也注意到了随着k的增大,三岔路口到来得越来越快,越来越密集。
从第一个三岔口k1开始:
k1=3
k2=3.44948697
k3=3.5440903
k4=3.5644073
k5=3.5687594......
仅仅从k的表面数值,费根鲍姆没有看出什么名堂,于是,他又算出相邻三岔路口间的距离d:
d1 = k2-k1 = 0.4495...,
d2 = k3-k2 = 0.0946...,
d3 = k4-k3 = 0.0203...,
d4 = k5-k4 = 0.00435...
从这些d之间,费根鲍姆好像看出点规律来!每次算出的下一个d,都大约是上一个d的五分之一!当然,并不是准确的五分之一,而是比例值差不多!好像有个什么常数在这儿作怪,多计算几项看看吧:
d1/d2 = 4.7514,
d2/d3 = 4.6562,
d3/d4 = 4.6683,
d4/d5 = 4.6686,
d5/d6 = 4.6692,
d6/d7 = 4.6694,
......
上面列出的这些比值都很接近,但又并不完全相同,两个相邻比值之间的差别却越来越小。费根鲍姆再计算下去,又多算了几项后,也只能得到一样的数值了,因为计算器的精度是有限的。
于是,费根鲍姆便作了一个猜测,这个比值,(Kn-Kn-1)/(Kn+1-Kn) 当n趋于无穷时,将收敛于一个极限值(也就是费根鲍姆常数):
δ=4.669201609......

同时,费根鲍姆也注意到,分岔后的宽度w也是越变越小,见图中所标示的w1、w2、w3等等(这个宽度从x=0.5测量,图中的红线)。那么,它们的比值是否也符合某个规律呢?
计算结果再次验证了费根鲍姆的想法,当n趋于无穷时,比值Wn/Wn+1将收敛于另一个 极限值:
α=2.502907875......
原来这两个分岔图存在两个常数,你要知道在物理里,往往一个新常数的出现往往能诞生新的概念,新的理论,像牛顿力学中的万有引力常数G,量子力学中的普朗克常数h等等。

费根鲍姆乐坏了,第一时间打电话告诉父母,自己发现了不平凡的东西,他要一鸣惊人了,他确实压抑太久了。
但是,费根鲍姆再次受挫,他将有关这两个常数的论文寄给物理期刊后,均被退稿,当时混沌的研究刚起步,审稿人没有重视这两个常数。尽管如此,费根鲍姆依旧继续研究。
他开始研究一个新的问题:除了逻辑斯蒂系统之外,在别的系统是不是也按照这个规律出现呢?
费根鲍姆再次拿起HP65计算器对对另一个简单的非线性系统(正弦映射系统): Xn+1 = k sin(Xn) 产生混沌的倍周期分岔过程作研究。
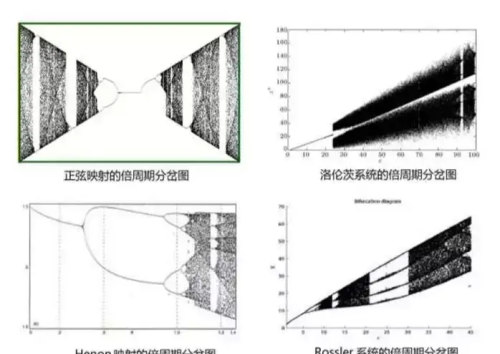
更多的倍周期分岔混沌系统
结果让费根鲍姆非常激动,问题的答案是肯定的。
正弦映射系统与逻辑斯蒂系统遵循着一模一样的规律。它们诞生的速度比值中都有一个同样的几何收敛因子:
δ=4.669201609......
分岔后的宽度也和逻辑斯蒂系统的分岔宽度,遵循同样的几何收敛因子而减小:
α=2.502907875......
正弦映射和逻辑斯蒂映射的迭代函数完全不一样,一个是正弦函数,另一个逻辑斯蒂映射,是二次的抛物线函数 :(Xn+1 = kXn·( 1-Xn))。
这个奇妙的事实说明,δ和α 两个费根鲍姆常数与迭代函数的细节无关,它们反映的物理本质应该是只与混沌现象、或者说是只与有序到无序过渡的某种物理规律有关,这就是学术界最后所领悟到、不得不承认的“费根鲍姆常数的普适性”。
一鸣惊人
1978年他发表了关于映射的研究的重要论文 《一个非线性变换类型的量子普适性》,其中特别谈到了对于混沌理论有直接意义的Logistic映射。费根鲍姆常数的发现,开启混沌普适性的研究,为混沌理论的研究作出了巨大贡献。
他,一个默默无闻的博士,被人口中的怪物成为了数学物理学家,开启了逆袭的人生。他的偏执、爱思考和对工作的疯狂是他成功的重要因素。
1982年,费根鲍姆被请回康奈尔大学做教授,回到了最初的起点,这次不是凭借麻省理工学院的名头混进去的,而是靠硬实力。

1986年,费根鲍姆获得沃尔夫物理奖,同一年,他受聘为洛克菲勒大学教授,直到如今。
逆袭不是两三天就能完成的事,或者是两三年,亦或者是二三十年。
不要停下前进的脚步,你现在也许还一事无成,但是要相信成功离你很近了。