如何让全球银行都破产,你只需要攻克黎曼猜想
导语:如何让全球银行都破产,你只需要攻克黎曼猜想
有人问过希尔伯特一个问题,说:“如果你沉睡了几百年,然后醒过来,你想干什么?”希尔伯特说,“我想问问有人把黎曼猜想证出来了吗?我太想知道了”。
如何让全球银行破产,是全球经济大萧条,还是战争摧毁了文明?都不是,你只需要破解黎曼猜想。
黎曼猜想是什么简单来说,黎曼猜想究竟讲了什么呢?就是一个寻找质数的方法。
什么是质数呢?我们应该在初中就学习过,就是指那些只能被1和自己所整除的数,如2、3、5、7、11等等。质数的研究属于数论的范畴。
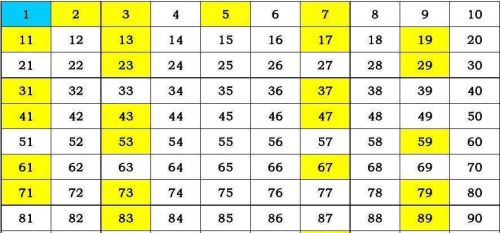
早在古希腊时期,欧几里得的《几何原本》中就有对质数的研究。欧几里得采用反证法证明了质数有无穷个,但是质数究竟有什么分布规律呢?欧几里得并没有找到。
至此之后,数学家们都费劲心思想要找寻质数分布的规律,1859年,黎曼发表了《论小于已知数的质数个数》论文探究质数分布的奥秘,这篇只有短短八页的论文就是黎曼猜想的“诞生地”。

论文手稿
在这篇论文中,黎曼通过研究,发现质数出现的频率的规律,提出了黎曼Zeta函数,黎曼Zeta函数是一个无穷级数的求和。
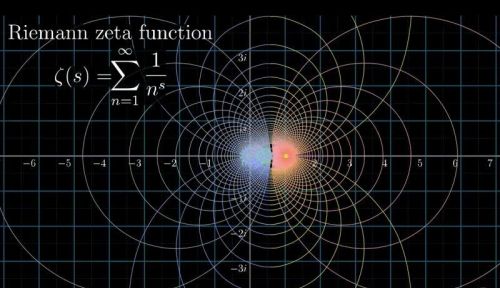
Zeta函数
黎曼对解析延拓后的Zeta函数证明了其具有两类零点。其中一类是某个三角sin函数的周期零点,这被称为平凡零点;另一类是Zeta函数自身的零点,被称为非平凡零点。针对非平凡零点,黎曼提出了三个命题。
第一个命题,黎曼指出了非平凡零点的个数,且十分肯定其分布在实部大于0但是小于1的带状区域上。
第二个命题,黎曼提出所有非平凡零点都几乎全部位于实部等于1/2的直线上。
而第三个命题就是重头戏了:很可能所有非平凡零点都全部位于实部等于1/2的直线上。
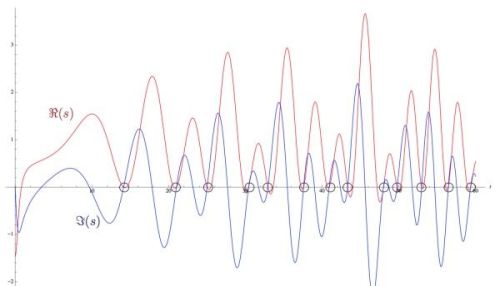
这第一个命题,黎曼表示太简单了,压根不需要证明,然而直到86年之后,第一个命题才由德国数学家蒙戈尔特在给出了完整的证明。
而至于第二个命题,黎曼声称自己已经证明,但是证明过程还需要简化,然而因为饱受病痛折磨,黎曼39岁就英年早逝,去世之后,他的手稿被管家付之一炬,自此黎曼的证明过程就彻底消失人间。
1932年。一位德国数学家Siegel整理黎曼仅存的手稿,让黎曼当时演算零点所用的公式重见天日,这个公式被命名为Riemann-Siegel公式。

凭借这个公式,数学家将第二个命题,推进到“至少有40%的非平凡零点在临界线上”,然后就再也没有新的进展了。

而第三个命题就是黎曼猜想,这条线,从此被称为临界线。关于第三个命题,即使是黎曼自己也不敢确定。即使到现在,也依然没有人能够给出答案。若黎曼猜想证明为真,则该函数的所有非平凡零点,即两图像的交点均会出现在该直线上。

黎曼猜想的完整表述
有一个数学研究所叫克雷研究所,2000年的时候他们给七道数学未解之谜分别给出了100万美元的悬赏,其中一道题就是证明黎曼猜想。如今18年过去了,7道题只有1道解决,黎曼猜想还是没能攻克。
 “黎曼猜想”后面是史诗级灾难
“黎曼猜想”后面是史诗级灾难从19世纪以来,越来越多的数学理论成果开枝散叶,很多早期被认为无用之用的分支,今日早已经成为现代科技最强有力的工具,为现代科技的发展推波助澜。
牛顿的微积分成为第一次工业革命的火炬,线性代数、矩阵分析、统计学、群论等为我们带来了信息文明,非欧几何(特别是黎曼几何)和张量分析让陆海导航成为可能,二进制让人类进入计算机时代。
而质数则成为了互联网大门的钥匙,替人类看护所有放在网络上的隐私,私钥加密、签名.....

数学家们之所以将质数应用在密码学上,正是因为人类还没有发现素数的规律,以它作密钥进行加密的话,即使运用超算,也会因求解质数时间过长而失去破解的意义。
现在普遍使用于各大银行的是RSA公钥加密算法 ,基于一个十分简单的素数事实:将两个大质数相乘,但是想要对其乘积进行因式分解却极其困难。
因为两个大素数的乘积因式分解时,除了1和其本身(这两个不在分解范围内)外,只有这两个大素数,但是分解时不知道这两个大素数,只有从最小的素数2开始,逐步试除,直到这两个大素数中较小的一个
这也是为什么全球各大银行都利用质素作为自己安全密码体系。

一旦素数之秘被解开,无需量子计算机,根据其原理甚至能破解现代银行的安全密码体系,让银行进入破产。
不仅是银行,那么现在几乎所有互联网的加密方式将不再安全,互联网变成一个裸奔的世界解。
所以数学家将对黎曼猜想的攻坚之路趣称为:“各大行长躲在银行保险柜前瑟瑟发抖,不少黑客则潜伏敲着键盘蓄势待发”。

黎曼猜想带来的危险不仅仅影响银行,更不仅仅是互联网, 甚至可能动摇对数学界产生影响。
在这数百年里,无数的数学家都在黎曼猜想上耗费过心力,数学文献中已有超过一千条数学命题以黎曼猜想的成立为前提。
如果黎曼猜想被证明,所有那些数学命题就全都可以荣升为定理;反之,如果黎曼猜想被否证,则那些数学命题中起码有一部分将成为陪葬品,被扫进历史的尘堆。
那些建立在黎曼猜想上的推论,可以说正在惶恐地等待着最终的审判。无论结果如何,都势必会影响数学大厦。
一个数学猜想与为数如此众多的数学命题有着密切关联,这是世上极为罕有的,也许正是因为这样的关系,黎曼猜想的名气和光环变得更加显著,也越发让人着迷。
 那放弃对黎曼猜想的破解吗
那放弃对黎曼猜想的破解吗不过和灾难相比,破解黎曼猜想更像是在诺亚方舟之中重获新生,被誉为数学届无冕之王的希尔伯特曾经说过:每一道数学难题都是会下金蛋的鹅。
就像对费马大定理的证明一样,它扩展了“无穷递降法”和虚数的应用;催生出库默尔的“理想数论”;促成了莫德尔猜想、谷山--志村猜想得证;拓展了群论的应用;加深了椭圆方程的研究;找到了微分几何在数论上的生长点;发现了伊利瓦金—弗莱切方法与伊娃沙娃理论的结合点;推动了数学的整体发展和研究,……同时又催生出一批又一批重量级数学家。

怀尔斯破解费马大定理
如果人类真的能够破解黎曼猜想,那么新的数学方法、新的数学规律、新的数学工具将会应运而生,带来人类走向新的文明。
希尔伯特曾经说过:“对我们来说没有什么不可知,以我的看法,对于自然科学来说也没有什么不可知。拋弃这个愚蠢的不可知,让我们决心反其道而行之。我们必须知道,我们必将知道。”
人类之所以能够不断发展,正是源于我们在不断掀开自然界中蕴藏着的所有奥秘。
