植树问题的三个公式(植树问题的三种情况)

带你一起搜罗小学数学里那些有趣的数学问题——

在植树问题里，要知道“每两棵树之间的距离”，我们简称“树距”或“间隔”，还要会分析“树距”与“树的棵树”（简称“棵数”）之间的关系。下面我们从“线路不封闭”和“线路封闭”两种情形展开探讨，可以根据题意画图理解。

涉及到的等量关系式有：

总线长＝树距×段数

段数＝总线长÷树距

树距＝总线长÷段数

一、线路不封闭

在不封闭的直线（曲线、折线、圆弧等）上种树。注意是一边还是两边种树

主要有以下三种情况：

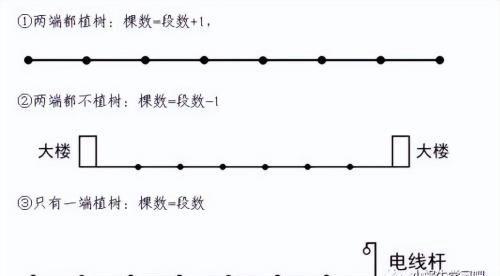
01 两端都种树

—

段数比棵数少1

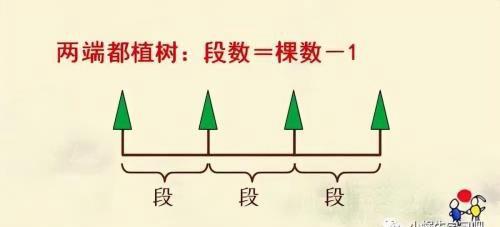
例：同学们在一条路的一旁植树，先植一棵树，以后每隔8米再植一棵，问第1棵和第6棵相距多少米

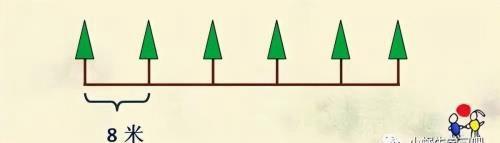
分析：此题是不封闭路线上求总线长的问题。因为两端都植树，所以：段数＝棵数－1。已知树距为8米，总线长＝段数×树距，即可求解：

分步列式：

①段数：6－1＝5（段）

② 总线长：5×8＝40（米）

综合算式：

8×（6－1）

＝8×5

＝40（米）

答：第1棵和第6棵相距40米。

02 两端都不种树

—

段数比棵数多1

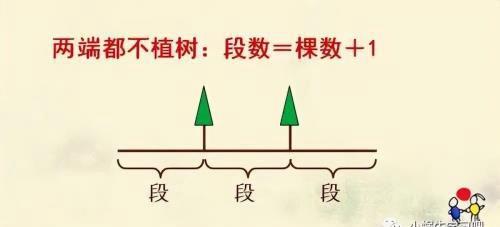
其实，爬楼梯、锯木头、截绳子、截钢管等和两端都不植树问题都是同一类题型。

锯木头：锯成的段数=锯的次数+1。

（锯木头问题）

爬楼梯：爬到几楼=爬的层数+1。

(爬楼梯问题)

例：两座楼相距30米，在两座楼之间有一条小路，现在要在路的两旁植树（路的两端都不植树），每隔5米种一棵，一共需要种多少棵树

分析：此题是不封闭路线上求“棵数”的问题。因为两端都不植树，所以：棵树=段数-1。已知树距为5米，需要先求出“段数”，段数＝总线长÷树距

分步列式：

①段数：30÷5＝6（段）

②一边种的棵数：6-1＝5（棵）

③两边一共种的棵树：5+5=10（棵）

综合算式：

（30÷5-1）×2

＝5×2

＝10（棵）

答：一共需要种10棵树。

03 一端种树一端不种

—

段数和棵数一样多

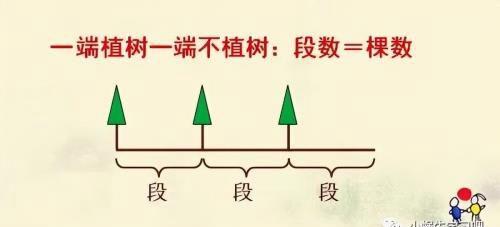
（前两种题型出现得比较多，这种题型出现得不多，提出来便于对比大家理解）

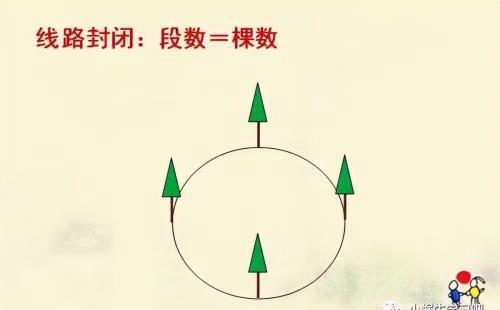
二、线路封闭

在闭合的曲线（长方形、梯形、矩形等闭合的曲线）上种树。

因为在闭合的曲线上两个端点是重合的，所以就相当于在不封闭的曲线上只有一端植树的情形。

段数和棵数一样多

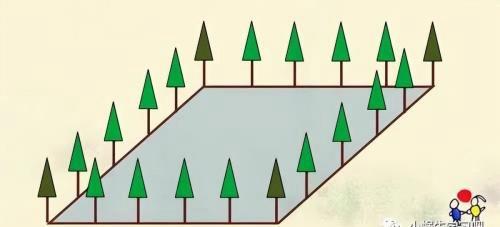
例：在一块操场四边种树，每边种6棵树，四边一共种多少棵树

01 方法一

—

分析：如果按每边都植树6棵，则四个角上的树重复计算了1次，应从总数之中减去。

分步列式：

①四边共有数（包含重复计算的棵数）：

6×4＝24（棵）

② 去除重复的棵数：

24－4＝20（棵）

综合算式：

6×4－4＝20（棵）

02 方法二

—

分析：封闭线路上植树，棵数和段数相等。

分步列式：

① 操场每边的段数：

6－1＝5（段）

② 四边共有的段数：

5×4＝20（段）

综合算式：

（6－1）×4＝20（段）

03 方法三

—

分析：先不计算四角上的4棵树，最后再加上。

分步列式：

①四边共有（不含四角上的棵数）：

（6－2）×4＝16（棵）

②加上四角上的4棵树：

16＋4＝20（棵）

综合算式：

（6－2）×4＋4

＝4×4＋4

＝16＋4

＝20（棵）

答：四边一共种了20棵树。

三、活学活用

—

1.在一条长300米的公路的一边安放路灯，每隔50米安放一个，这样需要放置多少个路灯

2.有一个圆形花坛，周长120米，现在每隔6米栽一株月季，一共可以栽多少株月季

3.李大爷在马路边散步，路边均匀地栽着一行树，李大爷从第一棵树走到第15棵树共用了7分钟，李大爷又向前走了几棵树后就往回走，当他回到第5棵树时共用了30分钟。李大爷步行到第几棵树时就开始往回走

4.某单位两座办公楼之间有一条长200米的道路，在道路起点的两侧和终点的两侧已各栽种了一棵树，现在要在这条路的两端栽种更多的树，使每一侧每两棵树之间的间隔不多于10米。如栽种每棵树需要50元人工费，则为完成栽种工作，在人工费这一项至少需要做多少预算

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小思创作整理编辑！