费马引理是充要条件吗(费马引理是什么函数都适用吗)

微分中值定理是高等数学中非常重要的一个章节。这一章节有很多重要定理。不知道历史上这些定理是如何一步步被证明的。不过教材上对微分中值定理的讲解大多是从费马引理开始…

费马引理

教材一般先用导数的定义和极限的保号性，证明费马引理。然后利用费马引理证明了罗尔定理。

罗尔定理

之后应用罗尔定理证明了拉格朗日中值定理和柯西中值定理。不管是拉格朗日中值定理还是柯西中值定理都是通过有目的的引入一个辅助函数，然后对这个辅助函数应用罗尔定理，很顺利地导出了拉格朗日中值定理和柯西中值定理。

拉格朗日中值定理

柯西中值定理

柯西中值公式中如果取F（x）=x，那么柯西中值公式就变成拉格朗日中值公式了。之后教材又应用柯西中值定理证明了洛必达法则的定理1。

洛必达法则（一）

洛必达法则（二）

最后又分别应用洛必达法则和柯西中值定理证明了带佩亚诺余项的n阶泰勒公式和带拉格朗日余项的n阶泰勒公式。

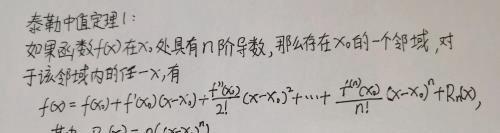
泰勒中值定理（一）

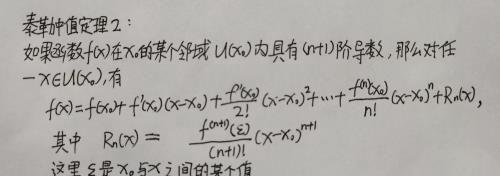
泰勒中值定理（二）

取x₀=0时的泰勒公式又叫做麦克劳林公式。而当n=0时带有拉格拉日余项的泰勒公式就变成了拉格朗日中值公式，因此可以说泰勒中值定理2是拉格朗日中值定理的推广。

高等数学中大概是这样一个思路把这些定理串接了起来。

仅仅是微分中值定理这样一个章节就有那么多以人名（费马、罗尔、拉格朗日、柯西、泰勒、麦克劳林）命名的引理、定理、法则。不禁让人感叹一套系统化的理论其实是经过很多能人不断积累不断优化才慢慢建立起来的。

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小茜创作整理编辑！