信息检索排序优方法(信息检索map)
排序算法在搜索引擎中非常重要,需要根据用户的查询 q,对一些相关的文档进行排序,尽可能地让用户感兴趣的文档排在前面。之前的文章介绍了一种 Learning to rank 的算法 RankNet,现在介绍另外两种比较经典的排序模型 LambdaRank 和 lambdaMART。
1.RankNet 的问题
信息检索排序问题常用的评价指标有 NDCG、ERR 等,不熟悉的童鞋可以看下之前的文章《信息检索评价指标》,这些评价指标是不平滑不连续的,无法直接用于梯度下降。RankNet 算法将排序问题转成一个概率问题,使用神经网络计算出一篇文章排在另一篇文章之前的概率,使用交叉熵作为损失函数,最后用梯度下降进行求解。
RankNet 的损失函数如下所示,本质上是计算样本的 pairwise error,即减少排序出错的样本数量,注意下式中 σ 是一个参数。

由于 RankNet 优化的是 pairwise error,因此会存在一些问题,我们先看下图。
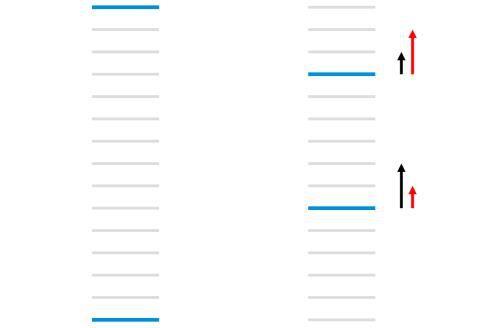
RankNet 的问题
在上图中包含 16 个文档,其中蓝色表示相关的文档,灰色表示不相关的文档。左图中 pairwise error 的个数为 13 (即第二个蓝色文档前有 13 个不相关文档),而右图 pairwise error 的个数为 11。RankNet 在优化时关注于文档对的错误,可能会出现有图的结果,但是很多时候这并不是理想的。
很多评价指标,例如 NDCG 和 ERR 等更加关注的时 top k 个结果的排序,因此优化过程中把相关文档往下调并不合适。
另外一点,右边的图中的黑色箭头表示 RankNet 下一次优化时调整的方向和梯度大小 (箭头越长梯度越大)。但是我们真正需要的是右边的红色箭头,即排名越靠前的文档梯度应该越大。因此微软提出了 LambdaRank。
2.LambdaRank
LambdaRank 是在 RankNet 基础上修改的,首先对 RankNet 的损失函数进行分解,得到其中的梯度。分解公式如下所示,wk 表示神经网络模型的参数。
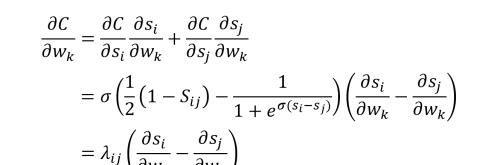
lambda 可以表示梯度的强度,lambda 可以进一步化简,假设对于训练集里面的文档对 (i, j),都有文档 i 排在文档 j 之前,即 Sij = 1,则 lambda 可以如下简化。
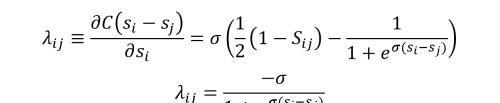
LambdaRank 主要创新点在于不直接定义模型的损失函数再求梯度,而是通过分析 RankNet 排序损失函数的梯度再直接对梯度 lambda 进行修改。
考虑到 NDCG、ERR 等指标不能直接求梯度,因此 LambdaRank 直接修改梯度 lambda,从而引入评价指标的信息,使梯度能够接近评价指标的表现。论文中的做法是交换两个文档 i,j 的位置,然后计算评价指标的变化情况 |ΔZ|,把 |ΔZ| 做为 lambda 的因子。Z 可以是 NDCG 等评价指标。
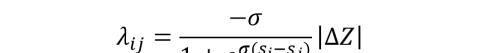
通过梯度 lambda 也可以反推出 LambdaRank 的损失函数,如下。
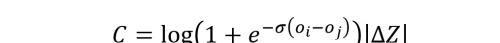
3.LambdaMART
LambdaMART 是一种结合了 LambdaRank 和 MART 的算法。MART 算法是一种集成学习算法,全称是 Multiple Additive Regression Tree,也称为梯度提升树 GBDT。MART 算法中每一棵树都是串联的关系,每棵树优化的是上一次分类器的残差。
3.1 MART 分类
对于样本 x,MART 预测的结果为 F(x),另 P+ 和 P- 分别表示模型预测正例和负例的概率,I+ 和 I- 表示真实的类标,如果 I+ = 1 (I- = 0),则表示正例;如果 I+ = 0 (I- = 1),则表示负例。可以定义交叉熵损失函数。
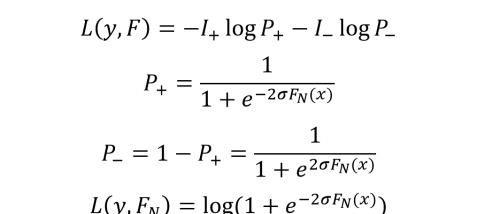
MART 每棵树拟合的是当前的负梯度,如下:
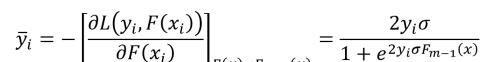
Rjm 表示第 m 棵树的第 j 个叶子节点包含的所有样本,则该叶子节点的取值可以如下计算,最小化对应的损失函数。对应的 gamma 值就是叶子节点的取值。
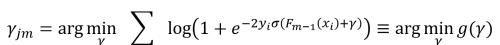
最终叶子节点的取值可以用牛顿迭代法求解,公式如下,具体推导过程可以参考论文《From RankNet to LambdaRank to LambdaMART: An Overview》。
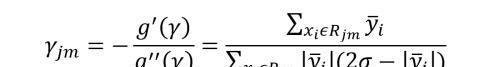
3.2 LambdaMART
LambdaMART 结合了 LambdaRank 和 MART,LambdaRank 中推导出 lambda 的公式
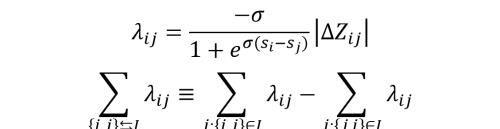
对应的损失函数如下。
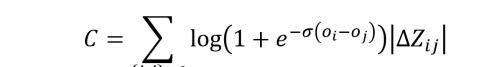
可以求出损失函数的一阶导数和二阶导数
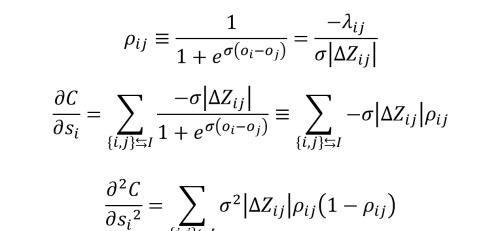
第 m 棵树的第 k 个叶子节点的取值用下面的公式进行计算。
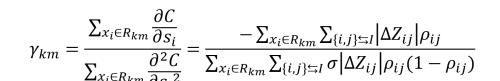
算法的伪代码如下图所示

4.参考文献
《From RankNet to LambdaRank to LambdaMART: An Overview》
《Adapting Boosting for Information Retrieval Measures》
《Learning to Rank with Nonsmooth Cost Functions》
免责声明:本文内容由互联网优秀作者用户自发贡献,本站仅提供存储空间服务,不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容,请与我们取得联系举报,一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑!