π是一个无理数,那么圆的周长也应是无理数,那么周长值还可以是整数吗,例如周长10?
这个问题很有意思,我来回答一下。
如果对数学有兴趣的朋友我推荐大家一本书,叫做《数学分析八讲》,这本书是著名的苏联数学家、教育学家辛钦写的,不厚,也几乎没有太多的公式,但是仔细读一下就会对很多数学问题有醍醐灌顶一般的感受。

人类本质上只知道什么是“整数”,这些数虽然无限多,但是是这个世界的一种非常明确的计量方法。而有理数就是通过这些整数构建出来的,表示为两个整数的商。有理数虽然有无限多个,但是依然不能填满整个数轴。
比如说我们常说的根号二( √2)就是一个无理数,这个数不能表示为两个整数的商。不过我们也可以说,其实根号二对我们来说并不是一个陌生的事物,因为根号二这个数字可以跟整数建立起来关系——也就是 √2* √2=2。而这些可以表示为整系数多项式的根的数叫做“代数数”。
从整数,到有理数,到代数数,我们似乎获得了数不尽的“数”,但是这些数不尽的数就能够把我们整个数轴填满吗?答案是:依然不能填满。
我们依然可以从数轴上找到一些无理数,这些无理数不是任何整系数多项式的根——也就是我们没有办法把这些数通过我们已有的数——整数“构造”出来。比如说圆周率π,比如说一个神奇的数——e。

确实有这些数,但是你没有办法把他们跟任何的整数关联起来,只能说,这是数轴上的一个数字,虽然我们不知道这个数具体是多少,又怎么通过我们已知的数把这个数字表示出来,但是这个数字确实存在,他的大小近似是3.1415926……。
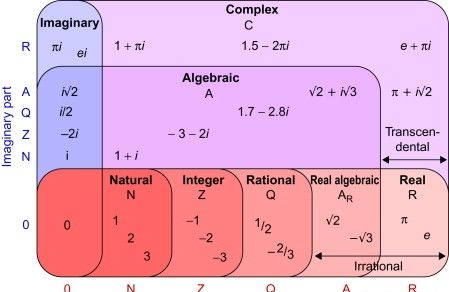
不可思议并且难以想象,但是这些不能表示但是又存在的数确实是实数的一部分的。这些数字就是“超越数”,超越数跟代数数之间的加减乘除和各种运算、超越数互相之间的加减乘除和各种运算都被囊括在“实数”内。
比如说,10/π存在吗?答案是,存在。这个数字就在数轴上,它的大小是
X.XXXXX
……这个数字的特点就是跟π相乘等于10,用这个数字作为圆的直径的时候,圆的周长是10。
你可能会奇怪,一个无理数10/π跟另一个无理数π相乘,怎么反而是一个有理数了?这个没办法,因为这个数字10/π确实存在,它的唯一定义就是:它是一个“跟π相乘结果等于10”的数,除此之外,没有任何意义。你不要管这个数字你写不写得出来,有多奇怪的性质,但是它就是存在——这就是数学不讲理、但是又符合逻辑的地方。
我们需要这个数,这个数字就出现了,我们只知道他在数轴上,但是除此之外对它一无所知——换句话,实数轴就是一个宝库,我们可以从中找到各种我们需要的东西,因为实数轴是“连续的”,上面有任何我们需要的数。
甚至于你说数轴上有通过有理数、代数数、超越数加在一起还构造不出来的数吗?这个其实我也不知道,你知道吗?
所以说,对数学不能较真,或者说数学本来就是超越我们“直观认识”的存在,有些时候只有定义,而没有你能够看到、感受到甚至于构造出来的“实体”。