代几综合题分几类题型(代数综合做题方法)

介绍4例代几综合题的解题过程，供大家参考。

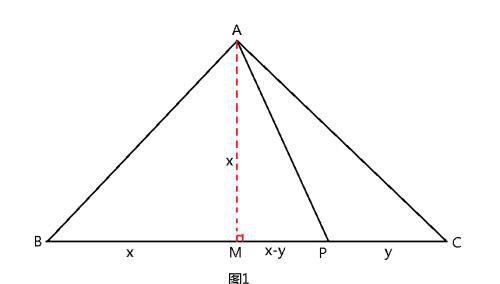
题目1：图1，在三角形ABC中，∠BAC=90°，AB=AC，P为BC上一点，求证PB²+PC²=2PA²。

解题过程：过A点作BC的垂线，垂足为M，BM=MC=MA。设BM=x，PC=y，则MP=x-y，MA=MC=x，PB=2x-y。

在Rt△AMP中，PA²=MA ²+MP²=x²+(x-y) ²=2x ²-2xy+y ²。

2 PA²=4x ²-4xy+2y ²=（2x）²-4xy+y ²+y ²

=（2x-y）²+y ²=PB ²+PC ²。

题目2：在直角三角形ABC中，∠BAC=90°，以AB、AC为边向三角形外分别作等边三角形ABD和ACE，连接DC、BE。设AB=x，AC=y，求DC·BE的值。

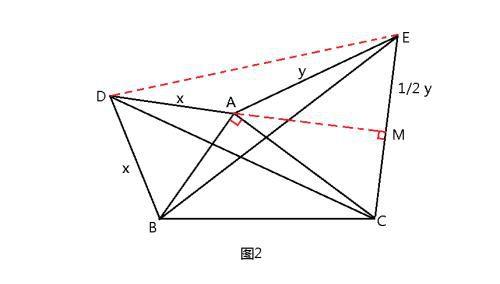
解题思路：如图2，连接DE，M为EC的中点，连接AM。∠DAE=∠DAC=∠BAE=150°。在△DAE、△DAC、△BAE中，两个等边三角形组成各边，故△DAE≌△DAC≌△BAE，DE=DC=BE。题目要求DC·BE的值，可以转化为求DE ²值。

我们知道，∠DAE=360°-60°-90°-60°=150°，∠EAM=30°，∠DAE+∠EAM=180°，D、A、M三点共线，DM⊥CE。

在Rt△DME中，EM=1/2y，DM=DA+AM=x+1/2y√3。

DE ²=EM ²+DM ²=（1/2y）²+（x+1/2y√3）²。

DE ²=x ²+y ²+√3 xy。

DC·BE= DE ²=x ²+y ²+√3 xy

题目3：如图3，在正方形ABCD中，以A为圆心，AB为半径作1/4圆，E为弧DB上一点，∠DEC=135°，求S△DEC与正方形ABCD面积之比是多少

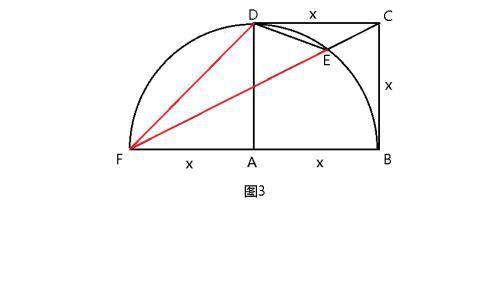
解题思路：如上图，FB为圆直径，连接FD、FC，圆周角DEF=1/2圆心角DAF=45°，

∠DEC+∠DEF=135°+45°=180°，故C、E、F三点共线。在△DEC和△FDC中，∠DCE为共角，弦切角CDE=∠DFC，△DEC∽△FDC。

设正方形边长为x，正方形面积为x²。

FC²=x²+（2x）²=5x²

S△DFC=1/2 x²

根据相似三角形面积比等于相似比的平方可得：S△DEC/ S△DFC=（DC/ FC）²=（x ²/5 x ²）=1/5

S△DEC/ S△DFC= S△DEC/1/2 x²=1/5

S△DEC/ x²=1/10

即三角形DEC与正方形ABCD面积比为1/10。

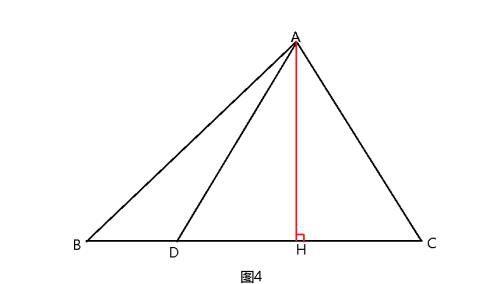
题目4：如图4所示，在三角形ABC中，点D是线段BC上的一点，连接AD。求证：

AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。

解题思路：过A点作AH⊥BC于H，在Rt△AHD和Rt△AHC中，根据勾股定理得：

AC²-HC²=AD²-DH²

AC²=AD²+HC²-DH²=AD²+（HC+DH）（HC-DH）= AD²+DC（HC-DH）= AD²+DC（DC-2DH）

AC²=AD²+DC ²-2DC·DH ①

用BD乘①式两边得：AC²·BD = AD²·BD +DC ²·BD -2DC·DH·BD ②

同理，在Rt△AHD和Rt△AHB中，根据勾股定理得：

AB ²-BH ²=AD ²-DH ²

AB ²=AD ²+BD ²+2DH·BD ③

用DC乘③式两边得：AB ²·DC = AD ²·DC +BD ²·DC +2DH·BD·DC ④

由②+④得：

AC²·BD+ AB ²·DC = AD²·BD +DC ²·BD -2DC·DH·BD + AD ²·DC +BD ²·DC +2DH·BD·DC= AD²·BD +DC ²·BD+ AD ²·DC +BD ²·DC

AB ²·DC+ AC²·BD= AD²（BD +DC）+ DC ·BD(DC+BD)= AD²·BC+ DC ·BD·BC

AB²·DC+AC²·BD-AD²·BC=BC·DC·BD。

该结论为斯特瓦尔特定理（Stewart定理），其证明过程稍显复杂，值得借鉴。

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小竹创作整理编辑！