> 房产
什么是概率论中的最大似然估计?
问:什么是概率论中的最大似然估计?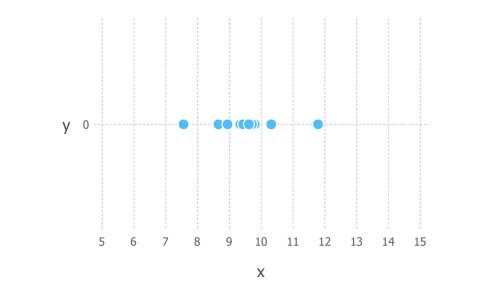
在统计学中,最大似然估计( MLE ) 是一种估计给定观察的统计模型参数的方法,方法是找到使给定参数的观察的可能性最大化的参数值。MLE 可以看作是最大后验估计(MAP) 的一种特殊情况,它假设参数的先验分布是均匀的,或者是 MAP 的一种变体,它忽略了先验,因此是非正则化的。
最大似然估计是一种确定模型参数值的方法。找到参数值使得它们最大化模型描述的过程产生实际观察到的数据的可能性。上面的定义可能听起来有点神秘,所以让我们通过一个例子来帮助理解这一点。
假设我们从某个过程中观察到了 10 个数据点。例如,每个数据点可以表示学生回答特定考试问题所需的时间长度(以秒为单位)。这10个数据点如下图所示

我们首先必须决定我们认为哪种模型最能描述生成数据的过程。这部分非常重要。至少,我们应该对使用哪种模型有一个很好的了解。这通常来自于拥有一些领域专业知识,但我们不会在这里讨论。
对于这些数据,我们假设数据生成过程可以用高斯(正态)分布充分描述。目测上图表明高斯分布是合理的,因为 10 个点中的大部分都聚集在中间,很少有点散布在左右两侧。(仅使用 10 个数据点即时做出此类决定是不明智的,但考虑到我生成了这些数据点,我们将采用它)。
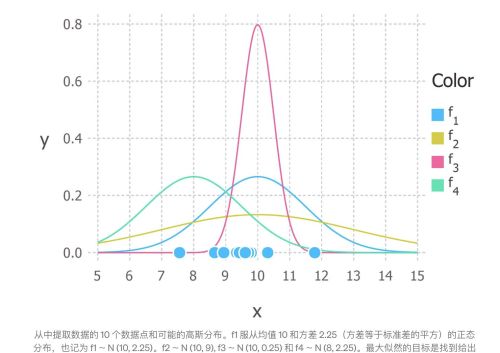
回想一下,高斯分布有 2 个参数。平均值 μ 和标准偏差 σ。这些参数的不同值会产生不同的曲线(就像上面的直线一样)。我们想知道哪条曲线最有可能产生我们观察到的数据点?(见下图)。最大似然估计是一种方法,它将找到 μ 和 σ 的值,从而生成最适合数据的曲线。

生成数据的真实分布是 f1 ~ N(10, 2.25),也就是上图中的蓝色曲线。
优秀作者:飞姐的口袋书