方程不难但要有多少种思路解题不易的方法(方程难不难)

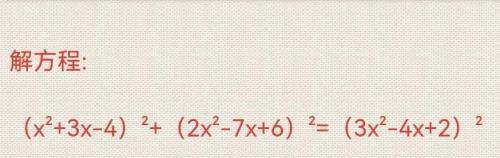
解法①:原方程可变为:

（x²+3x-4）²+2（x²+3x-4）（2x²-7x+6）+（2x²-7x+6）²=（3x²-4x+2）²+2（x²+3x-4）（2x²-7x+6）

∴（3x²-4x+2）²=（3x²-4x+2）²+2（x²+3x-4）（2x²-7x+6）

∴（x²+3x-4）（2x²-7x+6）=0

∴（x+4）（x-1）（2x-3）（x-2）=0

∴原方程的解为:x1=-4，x2=1，x3=3/2，x4=2

解法②:原方程变为:

-（x²+3x-4）²=0

∴（5x²-11x+8）（x²+3x-4）-（x²+3x-4）²=0

∴（4x²-14x+12）（x²+3x-4）=0

∴（2x²-7x+6）（x²+3x-4）=0

∴（2x-3）（x-2）（x+4）（x-1）=0

∴原方程的解为:x1=3/2，x2=2，x3=-4，x4=1

解法③：原方程变为:

²-（x²+3x-4）²-（2x²-7x+6）²=0

∴（x²+3x-4）²+2（x²+3x-4）（2x²-7x+6）-（x²+3x-4）²-（2x²-7x+6）²=0

∴2（x²+3x-4）（2x²-7x+6）=0

∴（x+4）（x-1）（2x-3）（x-2）=0

∴原方程的解为:x1=-4，x2=1，x3=3/2，x4=2

解法④：令x²+3x-4=a，2x²-7x+6=b，则3x²-4x+2=a+b

∴a²+b²=（a+b）²

∴ab=0

∴a=0或b=0或a=b=0

当a=0时，x²+3x-4=0，（x+4）（x-1）=0

∴x=-4或x=1

当b=0时，2x²-7x+6=0，（2x-3）（x-2）=0

∴x=3/2或x=2

当a=b=0时，不成立

∴原方程的解为:x1=-4，x2=1，x3=3/2，x4=2

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小芦创作整理编辑！