一元二次方程中的常见错误有哪些(一元二次方程中的常见错误解法)

欢迎关注：“黔中初数张文松”！

本文为你分享在《一元二次方程》一章的学习中常见的一些错误。

一、定义理解错误

例题：

错误分析：一元二次方程的定义中，“最高次数是二次”这个条件中实际包含了二次项系数不等于0，如果二次项系数为0，那么二次项也将不存在，也就不会有“最高次数是二次”，所以，我们在解答中务必要注意，二次项系数不为0这个隐含条件。此题的解答中，当k=2时，二次项系数k-2=0,所以k=2应舍去。故k=-2.

二、应用直接开平方法时的错误

例题： 若(a+b-2)²=25，求a²+b²的值.

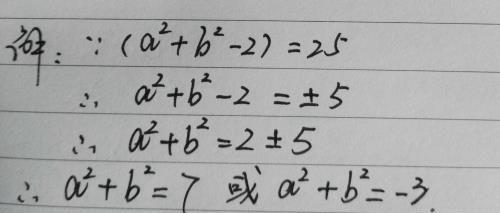
错误分析：我们知道，a²、b²都是非负数，而两个非负数的和仍然是非负数，所以a²+b²=-3是错误的。

三、应用配方法中的错误

例题：用配方法解方程：2x²-8x-10=0.

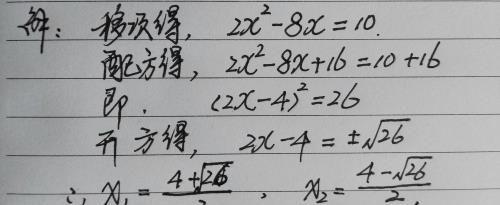
错误分析：配方法的关键是“当二次项系数是1时，将方程两边同时加上一次项系数的一半的平方”，此题二次项系数不为1，要先化为1.

四、应用公式法中的错误

例题：用公式法解方程：3x²-7x=2.

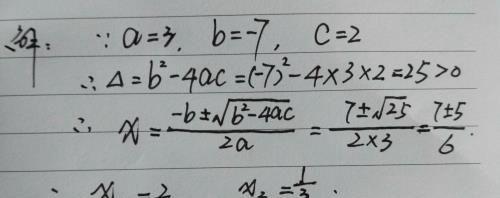
错误分析：用公式法解一元二次方程时，首先要将方程化为一般形式，以便确定a、b、c。此题还未化为一般形式，就确定a、b、c的值。所以导致错误。

五、应用等式性质时的错误

例题：解方程：5(2x-1)²=x(2x-1).

错误分析：此题是应用等式的性质来解方程。但忽略了等式性质中的条件，等式的两边同时除以同一个“不为0的数”，等式不变。所以，此题如果应用等式的性质来解，应分两种情况：(1)若2x-1=0,则得x=1/2,(2)若2x-1≠0，两边除以2x-1得，5(2x-1)=x,解得x=5/9.这样才不会漏解。

六、应用“根与系数的关系”时的错误

已知x1,x2是关于x的一元二次方程x²+(2k+1)x+k²+1=0的两个不同的实数根，且x1+x2=-x1x2.求k值.

错误分析：此题当k=0时，△＜0，而△＜0时方程不会有两个根。所以k=0应舍去。所以，当我们应用根与系数的关系来解答时要注意检查△，有时还要注意二次项系数。

七、题意理解不清

例题：某地区开展“科技下乡”活动三年来，接受科技培训的人员累计达95万人次，其中第一年培训了20万人次，求每年接受科技培训的人次的平均增长率是多少设每年接受科技培训的人次的平均增长率为x,则所列方程______________.

错误分析：此题的错误是把95理解成第三年的人数了。正确的列法是：20+20(1+x)+20(1+x)²=95.

我是“黔中初数张文松”！欢迎关注！欢迎留言！欢迎评论！

免责声明:本文内容由互联网优秀作者用户自发贡献，本站仅提供存储空间服务，不拥有所有权,不承担相关法律责任。若有涉嫌抄袭侵权/违法违规的内容，请与我们取得联系举报，一经查实立刻删除内容。本文内容由快快网络小舻创作整理编辑！