串联谐振电路原理？串联谐振电路怎么工作？案例公式，几分钟搞定

我是李工，希望大家多多支持我。

在之前已经有讲过各种振荡电路，Colpitts振荡电路、皮尔斯振荡电路、哈特利振荡电路、RC振荡电路、LC振荡电路。

还搞不懂LC振荡电路原理？看这一文就够了，图文结合，立马带你搞定

还不懂RC振荡器电路的原理？看这一文就够了，几分钟带你搞定

不会设计哈特利振荡器？图文+案例，手把手教你哈特利振荡器设计

皮尔斯振荡器电路工作原理图解，几分钟，立马搞定皮尔斯振荡电路

colpitts振荡器电路图分析，几分钟，立马搞定colpitts振荡器电路

振荡电路经常会提及到“谐振”，涉及到谐振电路和谐振频率，那到底是什么是谐振电路？谐振电路的工作原理是什么？这篇文章主要是关于谐振电路中的串联谐振电路，串联谐振电路的工作原理以及串联谐振电路的分析。

什么是串联谐振？

在串联谐振电路中，当电感的感抗等于电容的容抗值时，就会出现一个频率点。也就是说，X L = X C。

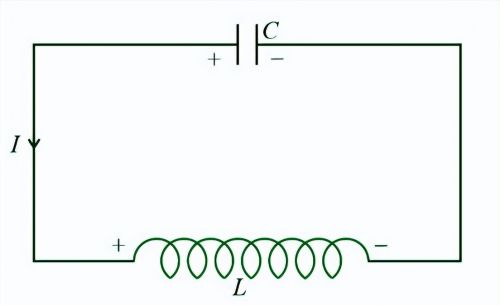
串联谐振电路

当X L = X C时，这个点就被称为电路的谐振频率点（f r），如果是在串联谐振电路上，这个频率会产生串联谐振。

串联谐振电路是电气和电子电路中最重要的电路之一，经常会应用在各种电路中，例如：交流电源滤波器、噪声滤波器、无线电和电视调谐电路中，这些电路产生了用于接收不同频道的选择性调谐电路。

什么是串联谐振电路？

下图显示的就是一个串联谐振电路。

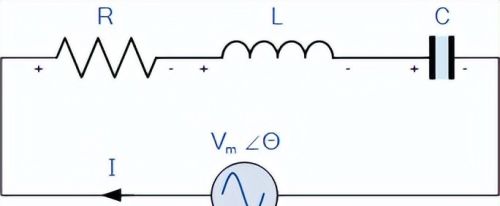
串联谐振电路

串联谐振电路的计算公式：容抗和感抗

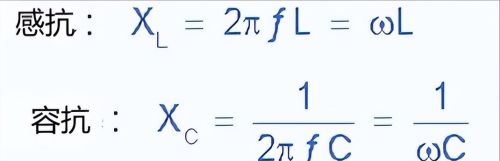
电路的容抗和感抗公式

当X L >X C时，为感性的。

当X L<X C时，为容性的。

串联谐振电路的计算公式：总电抗和总阻抗

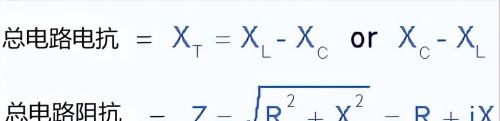
电路的总电抗和总阻抗公式

串联谐振电路的工作原理

下面这个动图可以很详细地解释串联谐振的工作原理。这个在上一篇文章中LC振荡电路中有详细地讲。

大家点击右侧标题直接跳转 ：LC串联谐振工作原理

串联谐振的工作原理

串联谐振电路案例

串联谐振网络由一个 30Ω 的电阻、一个 2uF 的电容和一个 20mH 的电感组成，连接在一个正弦电源电压上，该电源电压在所有频率下都具有 9 V的恒定输出。

计算谐振频率、谐振电流、谐振时电感和电容两端的电压、品质因数和电路带宽。还要画出所有频率的相应电流波形。

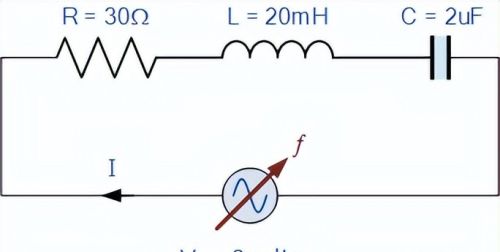
1、谐振频率，ƒ r

2.、谐振电路电流，I m

3、谐振感应电抗，X L

4、电感和电容两端的电压V L , V C

注意：电源电压可能只有 9 伏，但在谐振时，电容器 V C和电感器 V L两端的无功电压峰值为 30 伏！

5、品质因数，Q

6、带宽，BW

7、上下-3dB频率点， ƒH和ƒL

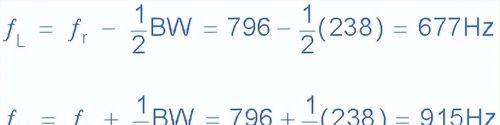
8、电流波形

串联谐振电路-电路波形图

串联谐振电路分析--对频率的感抗

从上面的感抗方程来看，如果频率或电感增加，则电感的总感抗值也会增加。随着频率接近无穷大，电感电抗也将向无穷大增加，电路元件就像开路一样。

然而，当频率接近零或直流时，电感的电抗会减小到零，从而导致相反的效果，就像短路一样。

这意味着感应电抗与频率“成比例”，在低频时很小，在高频时很高，具体的可以看下图：

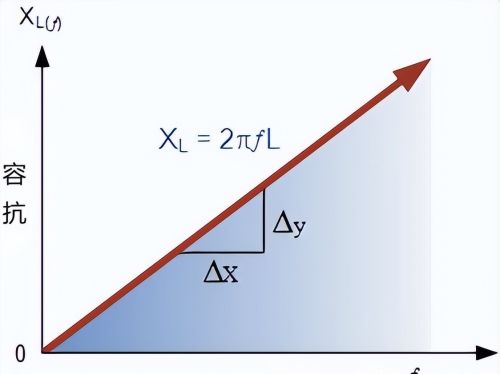
串联谐振电路分析--对频率的感抗

感抗与频率的关系图是一条直线线性曲线。电感的感抗值随着其两端频率的增加而线性增加。因此，感抗为正且与频率成正比 ( X L ∝ ƒ )

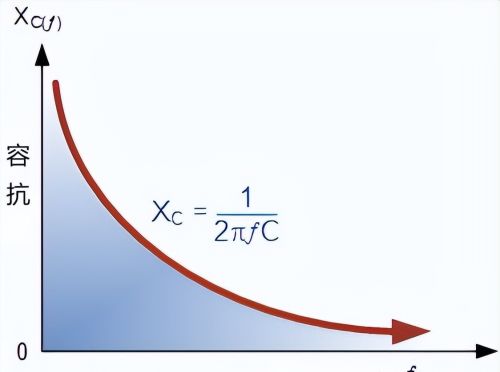
串联谐振电路分析--容抗频率

上面的容抗公式也是如此，但反过来。如果频率或电容增加，则总容抗会降低。随着频率接近无穷大，电容电抗将减小到几乎为零，导致电路元件像0Ω的完美导体一样工作。

但是随着频率接近零或直流电平，电容的电抗会迅速增加到无穷大，导致它像一个非常大的电阻一样，变得更像一个开路条件。这意味着对于任何给定的电容值，容抗与频率“成反比”，如下所示：

串联谐振电路分析--容抗频率

容抗与频率的关系图是一条双曲线。电容的电抗值在低频时具有非常高的值，但随着其上的频率增加而迅速减小。因此，容抗为负，与频率成反比 ( X C ∝ ƒ -1 )

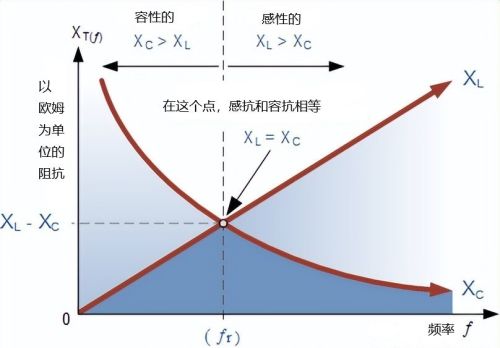
串联谐振电路分析--串联共振频率

我们可以看到，这些电阻的值取决于电源的频率。在较高频率时， X L较高，而在较低频率时，X C较高。那么一定有一个频点，X L的值与X C的值相同，并且存在。

如果我们现在将感抗曲线放在容抗曲线的顶部，使两条曲线在同一轴上，则交点将为我们提供串联谐振频率点（ ƒ r或ω r ），如下所示：

串联谐振电路分析--串联共振频率

其中：ƒ r以赫兹为单位，L以亨利为单位，C以法拉为单位。

当两个相反且相等的电抗的影响相互抵消时，交流电路中就会发生电谐振，因为X L = X C。上图中发生这种情况的点是两条电抗曲线相互交叉。

在串联谐振电路中，谐振频率ƒ r点可计算如下。

串联谐振电路谐振频率计算公式

然后我们可以看到，在谐振时，从数学上讲，两个电抗在 X L – X C = 0时相互抵消。这使得串联 LC 组合充当短路，与串联谐振电路中的电流流动的唯一相反是电阻，R。

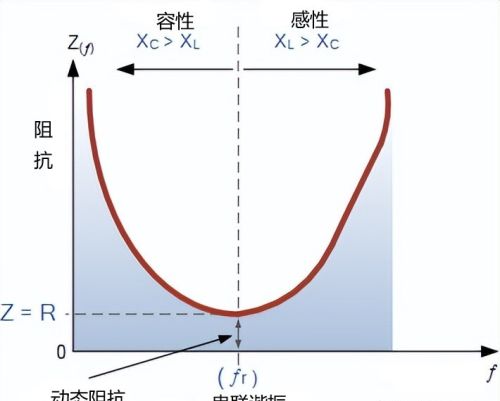
串联谐振电路分析--串联谐振电路中的阻抗

在复数形式中，谐振频率是串联 RLC 电路的总阻抗变为纯“实数”的频率，即不存在虚阻抗。这是因为在共振时它们被抵消了。所以串联电路的总阻抗就变成了电阻的值，因此： Z = R。

在谐振时，串联电路的阻抗处于其最小值并且仅等于电路的电阻R。谐振时的电路阻抗称为电路的“动态阻抗”，根据频率，X C（通常在高频下）或 X L（通常在低频下）将主导谐振的任一侧，如下所示。

串联谐振电路分析--串联谐振电路中的阻抗

要注意，当容抗主导电路时，阻抗曲线本身具有双曲线形状，但当感抗主导电路时，由于X L的线性响应，曲线是不对称的。

如果电路阻抗在谐振时处于最小值，则电路导纳必须处于最大值，串联谐振电路的特征之一是导纳非常高。这不是啥回事，因为谐振电阻值非常低意味着流经电路的电流可能非常高。

在串联谐振电路中，当V L = -V C时，产生的无功电压为零，并且所有电源电压都下降到电阻器上。因此，V R = V ，串联谐振电路被称为电压谐振电路（与并联谐振电路相反，并联谐振电路是电流谐振电路）。

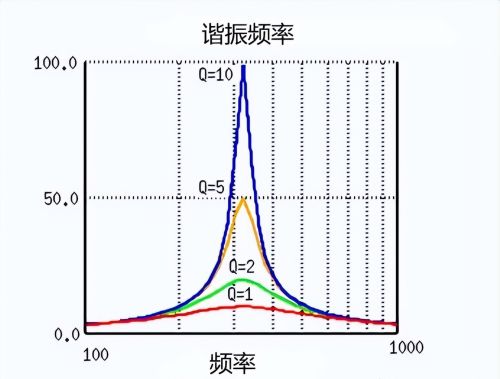
串联谐振电路分析--品质因数 Q

电流幅度的频率响应与串联谐振电路中谐振的“锐度”有关。峰值的锐度是定量测量的，称为电路的品质因数 Q。

品质因数将电路中存储的最大或峰值能量（电抗）与每个振荡周期期间消耗的能量（电阻）相关联，这意味着它是谐振频率与带宽的比值，电路Q越高，越小带宽，Q = ƒ r /BW。

串联谐振电路分析--品质因数 Q

由于带宽取在两个 -3dB 点之间，因此电路的选择性是衡量其抑制这些点任一侧的任何频率的能力的指标。选择性更强的电路将具有较窄的带宽，而选择性较低的电路将具有较宽的带宽。

串联谐振电路的选择性可以通过仅调整电阻值来控制，保持所有其他组件相同，因为Q = (X L或 X C )/R。

串联谐振电路总结为了在任何电路中发生谐振，它必须至少有一个电感和一个电容。当存储的能量从电感器传递到电容时，谐振是电路中振荡的结果。当X L = X C并且传递函数的虚部为零时发生共振。在谐振时，电路的阻抗等于电阻值Z = R。在低频时，串联电路是容性的：X C > X L，这使电路具有领先的功率因数。在高频下，串联电路是电感性的：X L > X C，这使电路具有滞后的功率因数。谐振时的高电流值会在电感和电容上产生非常高的电压值。串联谐振电路可用于构建高频选择性滤波器。然而，它的大电流和非常高的元件电压值可能会损坏电路。谐振电路的频率响应最突出的特点是其幅度特性中有一个尖锐的谐振峰。因为阻抗最小，电流最大，所以串联谐振电路也被称为接受器电路。 RLC串联谐振电路

对于一定频率称为谐振频率的串联 RLC 电路，在发生共振时，记住一下几点：

1、感抗X L等于容抗X C。

2、电路的总阻抗变为最小值，等于 R 即 Z = R。

3、随着阻抗减小，电路电流变为最大，I = V / R。

4、电感和电容两端的电压相互抵消，因此电阻两端的电压 V r = V，电源电压。

5、由于净电抗为零，电路变为纯电阻电路，因此电压和电流同相，因此它们之间的相角为零。

6、功率因数是统一的。

7、串联 RLC 电路中发生谐振的频率由下式给出

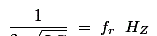
串联谐振频率计算公式

串联谐振频率计算公式

以上，就是关于串联谐振电路的相关知识以及分析，希望大家多多支持我。

图片来源于网络