工作点稳定放大电路频率之低频分析

我是电器电！接着上篇文章我们继续讲，如果是低频那么耦合电容C1C2要保留Cπ＇很小视为开路。Rb1∥Rb2很大可以忽略，Re＞＞Ce的容抗Re也可视为开路所以微变等效电路如下图示

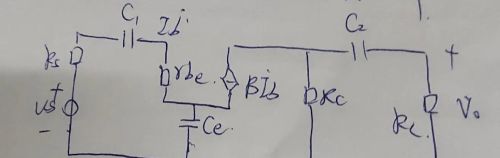
1

这种情况计算较复杂最好能把发射极极的Ce折算到基极回路

∵Xce＝（1＋β）×1／ωCe

∴Ce＝Ce＇／（1＋β）

电容值相当于降低了（1+β）倍

折算后C1与折算后的Ce＇串联后为

1／C1＇＝1／C1＋1／Ce

∴C1＇＝（C1xCe）／（1+β）C1＋Ce

变换后的等效电路如下图示

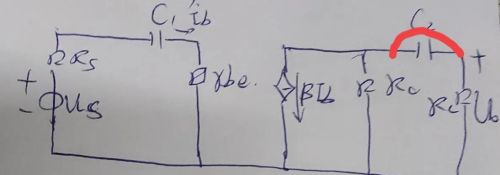
2

我们仔细看这个电路可以看到C1和rbe组成了一个高通电路既然是高通电路势必会有一个转折频率为下限截止频率fL1

fL1＝1／2πrbeC1＇ ① wL1＝1／rbeC1＇

再来看上面的图C2和RL又组成了一个高通电路所以又有一个下限截止频率fL2

fL2＝1／2π（RL＋RC）xC2②

ωL＝1／2π（Rc＋RL）×C2

比较一式和二式看分母，由于C1＇是串联小电容后得到的所以C1＇比C2小的多。（Rc＋RL）＞rbe所以fL1＞＞fL2既然是两个转折频率画出草图（演示图）如图示

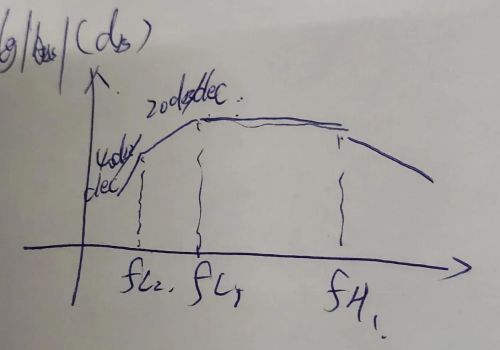
3

也就是说fL1时掉了3dB，到fL2时又掉了3dB如果fL1比fL2 大4倍以上那么我们取大的fL1做为下限截止频率。这时C2视为短路。如图2红线所示

这时的AuL＝－β（Rc∥RL）／rbe×rbe／rbe＋1／jωC＇

AuL＝Aum×jωrbeC1＇／（1＋jωrbeC1'）＝Aum[jω／ωL／（1+jω／ωL）]

幅频特性相频表达式

20lg｜AuL｜＝20丨g｜Aum｜＋20丨g（f／fL）／√1+（f／fL）＾2

相频特性表达式为

φ＝－180°＋90°－arctg（f／fL）

＝一90°－arctg（f／fL）

图和共发射极单管放大电路差不多如果fL1不大于fL2 4倍那么低频段有两个下限截止频率图就不画了。

最后非常感谢丈家的收看！