文氏电桥（RC）正弦波振荡电路（二）

我是电器电！这篇文章我们接着上文继续讲。让我们来推导一下RC正反馈网络的反馈系数是多大？也就是Ⅴf/VO是多少？图形可变为图形3如图所示

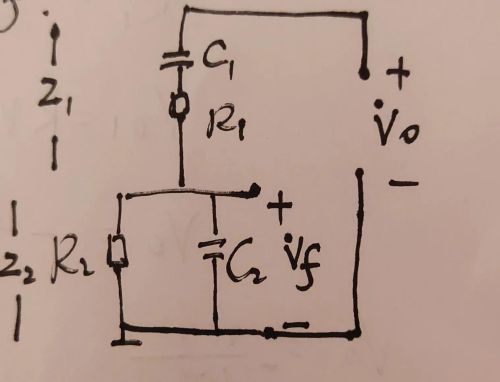
3

看3图可看出Z1=R1+1/jωC

Z2=〔R2∥（1/jωC2）〕=〔R2×（1/jωC2）〕/〔R2+1/jωC2〕同乘jωC2最后等于R2/（1+jωR2C2）

F=Vf/Vo=Z2/（Z1+Z2）=〔R2/（1+jωR2C2）〕/〔R1+（1/jωC〕+〔R2/（1+jωR2C2）〕=R2 /〔R1+（1/jωC）〕（1+jωR2C2）+ R2

=1 / （1+R1/R2+C2/C1）+ j（ωR1C2-1/ωC1R2）①

从①式中可看出实部为（1+R1/R2+C2/C1）虚部为j（ωR1C2-1/ωR2C1）看图3如果R1=R2=R，C1=C2=C，那么结果看起来就会比较容易①式就会变成②式

F=1/3+j（ωRC-1/ωRC）②从②式可看出如果虚部为0那么反馈系数的模最大。虚部为0那可么ωRC-1/ωRC=0， 可推出ω0=1/RC.③f0=1/2πRC，把f0信号加到两端此时反馈信号最大，这时就可推出幅频特性把③式代入①式则可得

|F|=1/√3^2+（ω/ω0-ω0/ω）^2

画出幅频特性如图所示

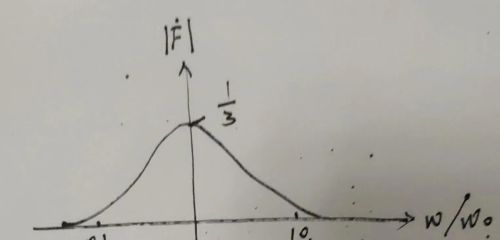
4

从4图幅频特性可看出横坐标为ω/ω0，当ω=ω0时，F的模最大为1/3。如果ω≠ω0时无论是大于还是小于那么反馈系数都会小于1/3.离中间越远反馈系数越小。

让我们再来看一下相频特性

φ=-arctg（ωR1C2-1/ωR2C1）/（1+R1/R2+C2/C1）=-arctg（ω/ω0-ω0/ω）/3

当ω=ω0时，虚部为0时，相位移为0度。VF与Vo同相，f=f0时反馈系数F=1/3，相频特性如图所示

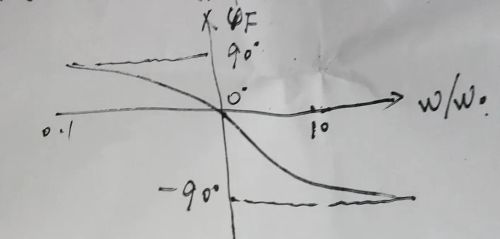
5

看5图当ω=ω0时，相位移为0度。ω>ω0时相位移滞后，ω＜ω0时，相位移超前。这篇文章先讲到这里，下一篇文章会讲到电路是如何起振的，希望大家关注收看！

最后非常感谢大家的收看！