电源经典运放电路，加法器，减法器，同向放大器，反向放大器

运算放大器组成的电路五花八门，令人眼花瞭乱。工程师在分析它的工作原理时常抓不住核心，令人头大。为此小编特地搜罗天下运放电路之应用，来个“庖丁解牛”，希望各位看完后有所收获。

遍观所有模拟电子技术的书籍和课程，在介绍运算放大器电路的时候，无非是先给电路来个定性，比如这是一个同向放大器，然后去推导它的输出与输入的关系，然后得出Vo=(1+Rf)Vi，那是一个反向放大器，然后得出Vo=-Rf*Vi。最后学生往往得出这样一个印象：记住公式就可以了！如果我们将电路稍稍变换一下，他们就找不着北了！

今天，教各位战无不胜的两招，这两招在所有运放电路的教材里都写得明白，就是“虚短”和“虚断”，不过要把它运用得出神入化，就要有较深厚的功底了。

虚短和虚断的概念

由于运放的电压放大倍数很大，一般通用型运算放大器的开环电压放大倍数都在80dB以上。而运放的输出电压是有限的，一般在10V～14V。因此运放的差模输入电压不足1mV，两输入端近似等电位，相当于“短路”。开环电压放大倍数越大，两输入端的电位越接近相等。

“虚短”是指在分析运算放大器处于线性状态时，可把两输入端视为等电位，这一特性称为虚假短路，简称虚短。显然不能将两输入端真正短路。

由于运放的差模输入电阻很大，一般通用型运算放大器的输入电阻都在1MΩ以上。因此流入运放输入端的电流往往不足1uA，远小于输入端外电路的电流。故通常可把运放的两输入端视为开路，且输入电阻越大，两输入端越接近开路。“虚断”是指在分析运放处于线性状态时，可以把两输入端视为等效开路，这一特性称为虚假开路，简称虚断。显然不能将两输入端真正断路。

在分析运放电路工作原理时，首先请各位暂时忘掉什么同向放大、反向放大，什么加法器、减法器，什么差动输入……暂时忘掉那些输入输出关系的公式……这些东西只会干扰你，让你更糊涂；也请各位暂时不要理会输入偏置电流、共模抑制比、失调电压等电路参数，这是设计者要考虑的事情。我们理解的就是理想放大器（其实在维修中和大多数设计过程中，把实际放大器当做理想放大器来分析也不会有问题）。

好了，让我们抓过两把“板斧”------“虚短”和“虚断”，开始“庖丁解牛”了。

反向放大器

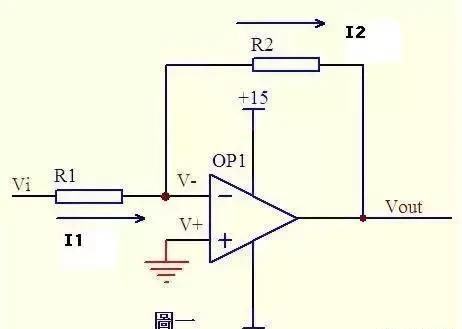
图1，运放的同向端接地=0V，反向端和同向端虚短，所以也是0V，反向输入端输入电阻很高，虚断，几乎没有电流注入和流出，那么R1和R2相当于是串联的，流过一个串联电路中的每一只组件的电流是相同的，即流过R1的电流和流过R2的电流是相同的。

流过R1的电流：

I1=(Vi-V-)/R1……a

流过R2的电流：

I2=(V--Vout)/R2……b

V-=V+=0……c

I1=I2……d

求解上面的初中代数方程，得：

Vout=(-R2/R1)*Vi

这就是传说中的反向放大器的输入输出关系式了。

同向放大器

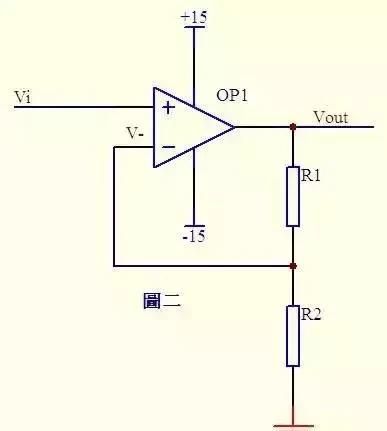
图2，Vi与V-虚短，则

Vi=V-……a

因为虚断，反向输入端没有电流输入输出，通过R1和R2的电流相等，设此电流为I，由欧姆定律得：

I=Vout/(R1+R2)……b

Vi等于R2上的分压，即：

Vi=I*R2……c

由abc式得：

Vout=Vi*(R1+R2)/R2

这就是传说中的同向放大器的公式了。

加法器1

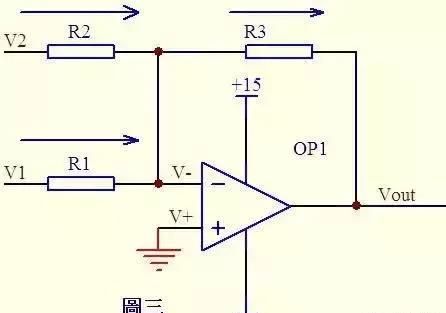
图3，由虚短知：

V-=V+=0……a

由虚断及基尔霍夫定律知，通过R2与R1的电流之和等于通过R3的电流，故：

(V1–V-)/R1+(V2–V-)/R2=(V-–Vout)/R3……b

代入a式，b式变为

V1/R1+V2/R2=Vout/R3

如果取R1=R2=R3，则上式变为：

-Vout=V1+V2

这就是传说中的加法器了。

加法器2

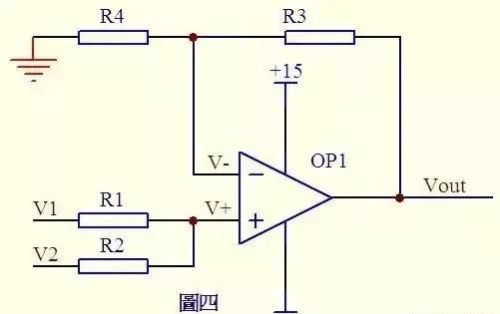
图4，因为虚断，运放同向端没有电流流过，则流过R1和R2的电流相等，同理流过R4和R3的电流也相等。故：

(V1–V+)/R1=(V+-V2)/R2……a

(Vout–V-)/R3=V-/R4……b

由虚短知：

V+=V-……c

如果R1=R2，R3=R4，则由以上式子可以推导出：

V+=(V1+V2)/2V-=Vout/2

故：

Vout=V1+V2

也是一个加法器！

减法器

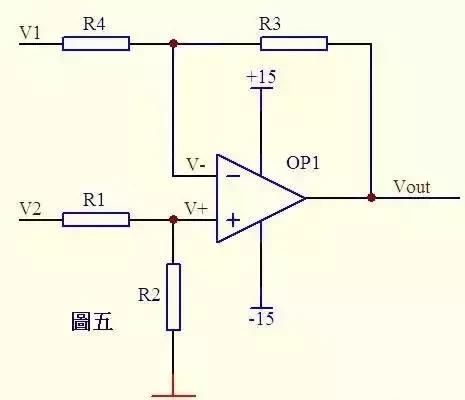
图5，由虚断知，通过R1的电流等于通过R2的电流，同理通过R4的电流等于R3的电流，故：

(V2–V+)/R1=V+/R2……a

(V1–V-)/R4=(V--Vout)/R3……b

如果R1=R2，则：

V+=V2/2……c

如果R3=R4，则：

V-=(Vout+V1)/2……d

由虚短知：

V+=V-……e

所以Vout=V2-V1，这就是传说中的减法器了。